
* 같이 보면 좋은 글
📄 삼각부등식
📄 사인법칙
* 코사인법칙 쉽게 외우는 법(증명 아님)
사인법칙은 사인함수와 외접원의 반지름과 관련이있다면,
코사인법칙은 두 변과 끼인각이 주어졌을 때 주로 사용합니다.
삼각형 ABC에 대하여 코사인법칙은 다음과 같습니다.

코사인법칙은 두 선분의 길이의 차와 피타고라스 정리의 모습을 모두 가지고 있습니다.
그 모습을 직관적으로 이해하면 코사인법칙 공식을 쉽게 암기할 수 있습니다.

그림으로 삼각형 ABC를 표현하면 다음과 같습니다.

a,b의 길이는 주어져 있으므로, 변 BC를 고정하면 점 A는 반지름의 길이가 b인 원 위를 돌게 됩니다.(원은 중심으로부터 거리가 일정하므로)
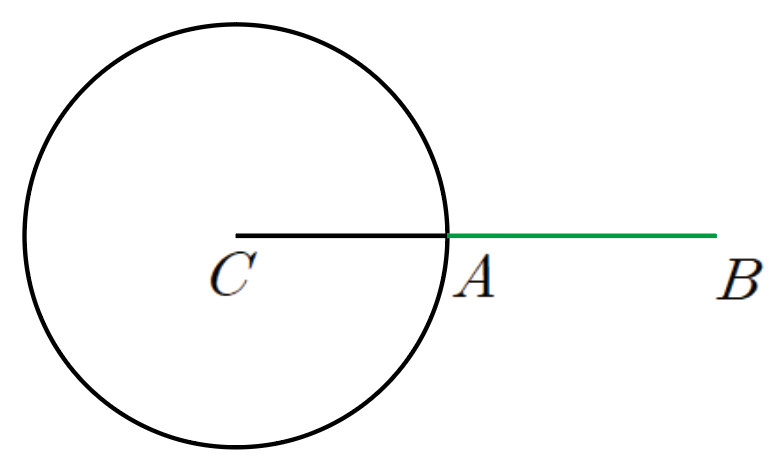
이때 C가 0도라면 A는 선분 BC 위에 있게 됩니다.따라서 선분 AB의 길이는 |a-b|가 됩니다.
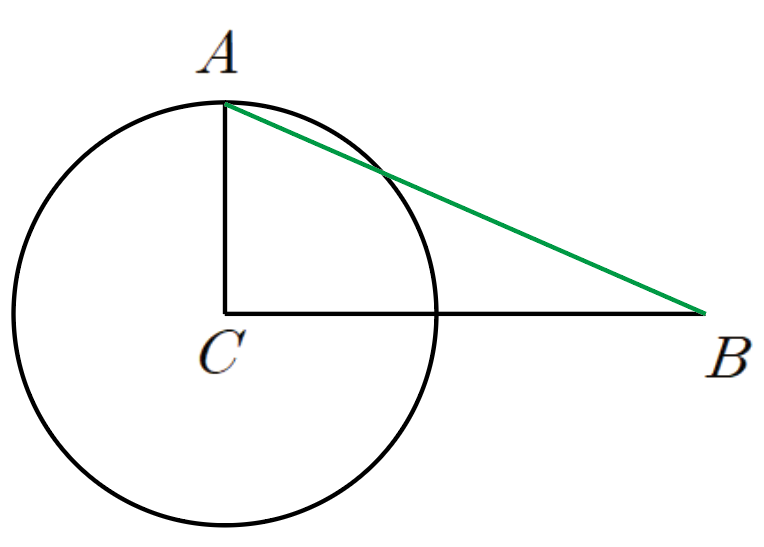
C가 90도라면 삼각형 ABC는 C가 직각인 직각삼각형을 만듭니다.이때 선분 AB는 빗변이므로 피타고라스의 정리를 만족시킵니다.
이를 직관적으로 암기하면

입니다.
[주의] 이 방법은 수학적으로 증명한 것이 아닙니다. 다만 어떻게 암기하면 쉽게 외울 수 있을지 방향성을 나타낸 것 뿐입니다. 공식을 외우는 도식으로만 사용하시길 바랍니다.
예) 삼각형 ABC에서 a=3, b=4, C=60º일 때, c를 구하시오.
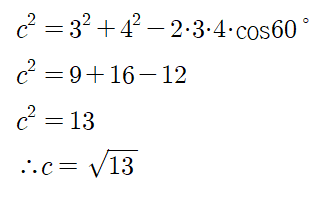
* 학습지 미리보기


* 첨부파일
* 닫는 말
이번 학습지는 코사인법칙으로, 코사인법칙을 이용해 변의 길이 또는 각의 크기를 구하는 문항으로 구성했습니다. 코사인법칙은 사인법칙과 마찬가지로 삼각함수를 이용해 도형의 구성요소를 파악할 수 있는 유용한 도구입니다. 코사인법칙을 익혀보고 교과서나 문제집에 있는 여러 문제를 해결해보시길 바랍니다.
✔ 이 글이 도움이 되셨나요?
- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.
- 학습지제작소를 구독하시면 빠르게 소식을 받아보거나 프리미엄 학습지를 신청하실 수 있습니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 고2, 고등학교 2학년, 수학I, 수1, 수I, 삼각함수, 코사인법칙, 코사인법칙 설명, 코사인법칙 학습지, 다운, 다운로드, pdf, 학습지제작소
'수학 학습지 > 수학I' 카테고리의 다른 글
| [수학I] 로그 밑변환 개념, 로그 밑변환 문제, 수학학습지 (0) | 2022.07.29 |
|---|---|
| 부분분수의 합 개념 + 수학학습지 | 부분분수 공식 [수학1/수학I] (1) | 2022.02.15 |
| [수학I] 33. 수열의 귀납적 정의 (개념+수학문제) (0) | 2020.12.15 |
| [수학I] 32. 시그마로 식의 값(다항식의 합) 계산하기 (개념+수학문제) (0) | 2020.12.11 |
| [수학I] 31. 수열의 합 ∑(시그마)의 뜻과 성질 (개념+수학문제) (0) | 2020.12.08 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 12. 26.
2020. 12. 26. 댓글
댓글
