인수분해 공식 완전정복 [중3 수학]

 

* 들어가며

인수분해란, 대상을 여러 요소의 곱으로 표현하는 것을 말해요.
예를 들어, 우리가 공부했던 소인수분해도 인수분해의 일종이라고 볼 수 있습니다.

$6=2 \times 3$에서

$6$을 그 구성요소인 $2$와 $3$의 곱으로 표현했으니까요.

 

그런 의미에서 초등학교 5학년에서 최소공배수를 찾는 방법에서도 인수분해 개념이 들어 있습니다.

해당 내용에서 10과 15의 최소공배수를 찾기 위해 자연수의 곱으로 나타내었었습니다.

[초5] 최소공배수 - 자연수의 곱으로 구하기

이처럼 자연수의 곱으로 표현하는 과정도 인수분해의 일종입니다.

 

* 다항식의 인수분해

반응형

통상 중학교 이상 수학에서 인수분해는 다항식을 대상으로 합니다.

다항식을 다항식의 곱으로 표현하는 거죠.

예를 들어, $ma+mb$를 $m(a+b)$로 묶어 표현했다면,

$m \times (a+b)$이므로 인수분해로 볼 수 있습니다.

 

이와 같은 인수분해 식으로는 다음과 같습니다.

1) $ma+mb = m(a+b)$

2) $a^2 +2ab + b^2 = (a + b)^2$

3) $ a^2 -2ab + b^2 = (a - b)^2 $

4) $ a^2 - b^2 = (a+b)(a-b) $ //합차공식

5) $ x^2 + (a+b)x + ab = (x+a)(x+b) $

6) $ acx^2 +  (ad+bc)x + bd = (ax+b)(cx+d)$

 

문제 $x^2 + 4x +4$를 인수분해하시오.

➡  $x^2 + 4x +4 = x^2 + 2 \times 2 \times x + 2 \times 2$이므로 $(x+2)^2$입니다.

 

 

 

문제 $a^2 - 9$를 인수분해하시오.

➡ $a^2 - 9 = a^2 - 3^2$이므로 $(x+3)(x-3)$입니다.

 

 

 

문제 $x^2 -8x + 15$를 인수분해하시오.

➡  $(-3)+(-5)=-8$,  $(-3) \times (-5) = 15$이므로

$(x-3)(x-5)$로 인수분해할 수 있습니다.

 

 

계수를 놓고 인수분해하기

위 그림과 같이 계수를 놓고 대각선으로 곱해 일차항의 계수를 놓고 비교해볼 수도 있어요.

$x^2$의 계수는 1이므로 왼쪽에 1,1을 놓고

상수항의 계수는 15이므로 오른쪽에 1,15나  3,5를 놓을 수 있겠죠?

그런데 대각선으로 곱했을 때 계수가 음수가 나와야하니까

오른쪽에는 -1, -15 또는 -3, -5가 나와야 합니다.

그 중 더해서 일차항의 계수가 -8인 경우는 -3, -5이므로

오른쪽에는 -3, -5를 적습니다. 따라서 인수분해한 식은 $(x-3)(x-5)$입니다.

 

 

 

문제 $6x^2 -x  -2 $를 인수분해하시오.

➡ 문제 해결을 위해 $ acx^2 +  (ad+bc)x + bd = (ax+b)(cx+d)$ 인수분해 공식을 활용해야 합니다.

위 문제와 마찬가지로 계수를 놓고 대각선으로 곱해보면

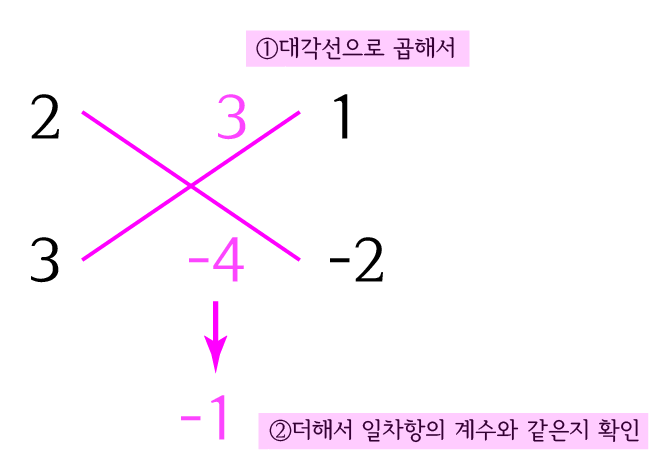
일차항의 계수가 -1인 경우를 찾을 수 있습니다. 따라서

$(2x+1)(3x-2)$입니다.

 

 

* 인수분해 연습문제 학습지 모음

지금까지 중3 수학 인수분해 공식들을 살펴보았습니다.

예제와 같이 인수분해 공식을 활용해 인수분해하거나

계수를 놓고 대각선으로 곱하는 방법으로 인수분해한 식을 찾는 연습이 필요합니다.

 

아래에 인수분해 연습문제지를 올려드리니 학습에 참고 바랍니다.

 ** 인수분해 연습문제

 ** 인수분해 유형연습 1 : 완전제곱식 $(a^2+2ab+b^2)$꼴로 인수분해하기

 ** 인수분해 유형연습 2 : $(x+a)(x+b)$꼴로 인수분해하기