안녕하세요, 학습지제작소입니다.
이번 포스팅은 수학I 네 번째 학습지로, 로그의 연산에 대해 이야기해보려고 합니다.
지난 세 번째 학습지에서는 로그의 의미를 공부해보았는데요,
오늘은 로그의 합, 차, 곱 등 로그가 연산기호와 만나면 어떤 변화가 일어나는지 공부해봅시다.
| 로그끼리 더하면 어떻게 될까?
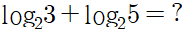
위 문제와 같이 밑이 같은 로그를 더하면 어떻게 될까요?
합을 구하기 위해 로그의 정의로 돌아가봅시다.
로그는 밑을 a, 진수를 N으로 가질 때, 다음 식이 성립합니다.


log_2 3을 x, log_2 5를 y로 놓으면 x,y가 각각 지수인 두 식을 구할 수 있습니다.

이 상태에서 두 식을 서로 곱하면 지수가 x+y인 식을 구할 수 있고, 그 값이 15임을 알 수 있습니다. 이 상태에서 다시 로그의 정의를 떠올려 로그로 나타내면 2는 밑으로, 15는 진수가 됩니다.
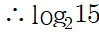
결과를 살펴보면, 밑이 서로 같은 두 로그의 합은 곱이 진수인 로그가 됩니다.

| 로그끼리 빼면 어떻게 될까?
반대로 로그끼리 빼 봅시다. 역시 비슷한 예제를 가져와 보았습니다.

두 수를 역시 x,y로 나타내어봅시다.
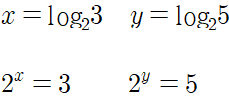
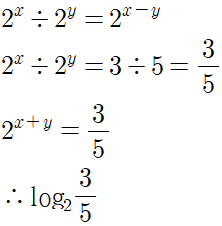
로그의 뺄셈의 값의 진수는 5분의 3으로, 진수였던 3을 5로 나눈 몫임을 알 수 있습니다. 로그의 뺄셈은 진수끼리의 나눗셈을 진수로 갖는 로그가 차가 됩니다.
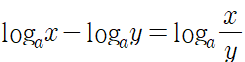
| 진수가 거듭제곱이라면?
진수가 거듭제곱꼴이라면 어떻게 간단히 나타낼 수 있을까요?
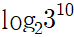
위 로그를 간단히 나타내기 위해 로그의 정의를 활용해봅시다.

이와 같이 나타낼 수 있는데요, 좌변과 우변의 수가 서로 같으므로, 10제곱근 근호를 씌울 수 있습니다.
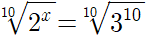
n제곱근 근호는 지수법칙에 의해 지수의 분모로 이동하므로,

이 됩니다. 이를 로그로 다시 표현하면,

입니다. 우리가 구할 것은 x의 값이므로 양변에 10을 곱합니다.
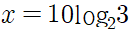
따라서 log_2 3에 10이 곱해져 있는 수가 됩니다. 이 식을 자세히 살펴보면, 기존 진수에 있던 지수 10이 로그 앞으로 나와있음을 알 수 있습니다.

따라서 위 식이 성립합니다.
| 밑변환(진수의 나눗셈)
로그의 덧셈과 뺄셈은 밑이 서로 같을 때에 계산할 수 있습니다. 우리는 필요에 따라서 밑을 바꿀 필요가 있는데, 밑변환 과정에 따라 밑을 바꿀 수 있습니다.
한번 밑이 2, 진수가 3인 로그를 다르게 표현해봅시다. (단, a는 0이상 실수, a는 1이 아님)

로그를 x으로 표현해보면 2의 x제곱과 3이 같음을 알 수 있습니다. 여기에 밑이 a인 로그를 씌우면 좌변의 x가 로그 앞으로 나옴을 볼 수 있습니다. 이때 x와 로그는 곱으로 이루어져 있으므로 양변을 log_a 2로 나누면 위와 같은 값을 얻을 수 있습니다. 우리는 이를 밑변환이라고 부릅니다.
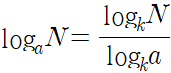
때에 따라 밑이 10인 상용로그로 취하기도 하는데요, 상용로그는 밑을 생략하기 때문에 더 간결한 형태로 쓸 수 있습니다.

여러 로그를 밑변환해봅시다.
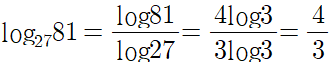

이와 같이 밑을 바꿈으로써 간단히 표현할 수 있습니다.


이번 문제는 로그의 덧셈, 뺄셈, 밑변환 등 여러 로그의 연산을 풀어볼 수 있도록 준비했습니다.
첨부파일은 아래와 같습니다.
이상으로 로그의 연산 포스팅을 마치겠습니다.
오늘도 즐거운 하루 보내세요!
#태그 수학1, 고등학교 2학년 수학, 고2수학, 지수함수와 로그함수, 지수, 로그, 밑변환, 밑변환 공식, 로그의 덧셈, 로그의 뺄셈, 로그 연산 문제, 다운, 다운로드, 학습지제작소
'수학 학습지 > 수학I' 카테고리의 다른 글
| [수학I] 6. 상용로그로 자릿수 구하기 (개념 + 수학문제) (0) | 2020.03.11 |
|---|---|
| [수학I] 5. 상용로그의 성질, 밑변환, 값 구하기 (개념+수학문제) (1) | 2020.03.07 |
| [수학I] 3. 로그, 밑, 진수의 뜻 (개념+수학문제) (2) | 2020.02.29 |
| [수학I] 2. 지수의 확장 (2) : 무리수인 지수의 계산 (개념+수학문제) (2) | 2020.02.26 |
| [수학I] 1. 지수의 확장 (1) : 유리수인 지수의 계산 (개념 + 수학문제) (0) | 2020.02.20 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 3. 3.
2020. 3. 3. 댓글
댓글
