
안녕하세요, 학습지제작소입니다.
오늘은 고등학교 2학년 수학 I을 포스팅해보려고 합니다.
벌써 세 번째 포스팅이네요.
지금까지 지수의 확장에 대해 이야기해보았었는데요,
관심있으신 분들은 아래 링크를 활용하시길 바랍니다.
<수학 I 지수 개념설명-문제 보기>
[수학I/수학문제] 1. 지수함수와 로그함수 > 지수의 확장 (1)
안녕하세요, 학습지제작소입니다. 오늘은 고등학교 2학년 연산문제를 포스팅해보려고 합니다. 고등학교 2학년 수학 I 과목에서는 1) 지수함수와 로그함수 2) 삼각함수 3) 수열 을 공부하는데요, 세 단원 모두 함수..
calcproject.tistory.com
[수학I/수학문제] 2. 지수함수와 로그함수 > 지수의 확장 (2)
안녕하세요, 학습지제작소입니다. 이번 포스팅은 고등학교 2학년 수학 I 1단원 지수함수와 로그함수 두 번째 학습지를 공유하고자 합니다. 이번 주제 역시 지수의 확장이며, 지수가 유리수인 경우에서 나아가 무리..
calcproject.tistory.com
오늘은 로그에 대해 공부해 볼 차례인데요, 로그는 고등학교에서 배우는 새로운 연산 중에 하나이기 때문에, 로그 자체의 의미를 깊게 살펴볼 필요가 있습니다.
오늘은 로그의 의미에 대해 알아보고, 로그의 구성요소에 대해 살펴본 후, 여러 예제를 풀어보는 순서로 공부해봅시다.
1. 로그의 의미
1) 왜 단원명이 지수함수와 로그함수일까?
수학 I의 1단원은 지수함수와 로그함수입니다. 그리고 우리는 지수에 대해 배운 적이 있습니다. 그렇다면 왜 교육과정에서는 지수와 로그를 한데 묶어놓는 것일까요? 그 까닭을 알기 위해서는 밑, 지수와 값의 관계에 대해 알 필요가 있습니다.
지수의 장점은 무엇이었을까요? 지수는 큰 수를 간단히 나타낼 수 있다는 점에서 굉장히 유용한 수학 요소입니다.
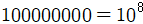
그렇다면 큰 수를 작게 나타낼 수 있는 방법은 없을까요? 밑과 지수로 큰 값을 만들었다면, 큰 값과 밑으로 지수를 표현한다면 효율적으로 수를 표현할 수 있습니다. 이것이 로그입니다.
2) 로그의 의미
조금 더 자세히 이야기해본다면, 로그의 정의는 밑을 a, 지수 x로 표현할 수 있는 수 N에 대하여,
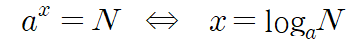
로 표현할 수 있습니다. 즉, N을 a를 밑으로 가질 때 지수의 값이 로그입니다.
예)

2. 로그의 구성요소
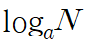
1) 밑
위 로그에 대하여 a를 밑이라고 부릅니다.
밑은 0이상의 실수이며, 1이 될 수 없습니다. 1이 되지 않는 까닭은 N이 1이 아니라면 어떠한 거듭제곱도 N을 만들 수 없기 때문입니다.

따라서 밑 a에 대한 조건은
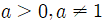
입니다.
2) 진수
위 로그에 대하여 N을 진수라고 부릅니다.
진수는 0이상의 실수입니다. 진수가 양의 실수인 까닭은 양의 실수인 밑을 어떻게 거듭제곱하더라도 0이하의 수를 만들 수 없기 때문입니다.
따라서 진수 N에 대한 조건은

입니다.
3. 로그 값 구하기
자연수 a,N에 대하여 우리는 로그 값을 구할 수 있습니다.
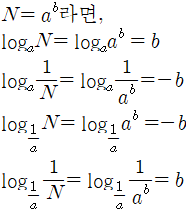
밑, 진수가 자연수/단위분수인 경우, 위와 같이 로그 값을 구할 수 있습니다.
예)
$\log_2{8} = \log_2{2^3} = 3$
$\log_2{\cfrac{1}{4}} = \log_2{2^{-2}} = -2$
$\log_{\frac{1}{3}}{9} = \log_{\frac{1}{3}}{3^{2}} = -2$
$\log_{\frac{1}{5}}{\cfrac{1}{25}} = \log_{\frac{1}{5}}{\cfrac{1}{5^2}} = 2$
그리고, 밑이나 진수에 근호가 붙어 있거나, 소수인 경우에는 다음과 같이 로그 값을 구합니다.

예)
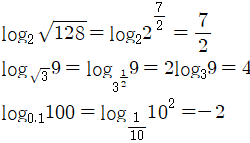
이와 같이 로그 값은 밑을 진수로 만드는 지수 값입니다.
그리고, 밑이 3 진수가 5인 경우처럼 특정한 유리수로 표현할 수 없는 경우도 있습니다. 이런 경우에는 로그를 붙여 그대로 사용합니다.

오늘의 학습지는 오늘 살펴본 유형을 문제로 제시하여, 로그의 의미를 생각해보고 값을 구해봄으로써 양감을 다질 수 있도록 준비했습니다. 로그는 새로운 연산이므로, 반복적인 연습을 해야 추후 로그의 연산에서 헷갈리지 않을 수 있습니다.
학습지 첨부파일은 아래와 같습니다.
그럼 다음 포스팅 때 뵙겠습니다~
감사합니다 :)
#태그 : 지수함수와 로그함수, 수학 I, 지수, 로그, 로그의 의미, 로그 개념, 로그 개념설명, 로그 연습문제, 로그 연산문제, 다운, 다운로드, 학습지, 로그 학습지, 고2 수학문제, 고2 학습지, 학습지제작소
'수학 학습지 > 수학I' 카테고리의 다른 글
| [수학I] 6. 상용로그로 자릿수 구하기 (개념 + 수학문제) (0) | 2020.03.11 |
|---|---|
| [수학I] 5. 상용로그의 성질, 밑변환, 값 구하기 (개념+수학문제) (1) | 2020.03.07 |
| [수학I] 4. 로그의 성질, 로그가 들어간 공식 (개념+수학문제) (2) | 2020.03.03 |
| [수학I] 2. 지수의 확장 (2) : 무리수인 지수의 계산 (개념+수학문제) (2) | 2020.02.26 |
| [수학I] 1. 지수의 확장 (1) : 유리수인 지수의 계산 (개념 + 수학문제) (0) | 2020.02.20 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 2. 29.
2020. 2. 29. 댓글
댓글
