
* 같이 보면 좋은 글
* 도함수
도함수는 미분가능한 함수 f(x)에 대하여,
h가 0으로 가까이 갈 때,
(x, f(x)), (x+h, f(x+h))의 순간변화율을 나타낸 함수입니다.
(미분가능한 함수에 대해서는 추후 '연속함수'와 함께 묶어서 설명하겠습니다.)
순간변화율(미분계수)는 극한값을 구하는 과정이라면,
도함수는 x에 대한 미분계수를 함수로 나타낸 것입니다.
이와 같이 미분가능한 함수의 도함수를 구하는 것을 미분이라고 합니다.
때문에 도함수를 구하는 과정은 미분계수와 유사합니다.

도함수는 y=x^n(x의 n제곱)의 도함수를 구할 수 있으면 간편하게 구할 수 있습니다.
우선 (x+h)의 제곱, 세제곱, 네제곱, n제곱을 내림차순으로 놓았을 때 두 번째 항까지 나타내어봅시다.

이를 이용하여 y=x^2, y=x^3, y=x^4...의 도함수를 나타내면,
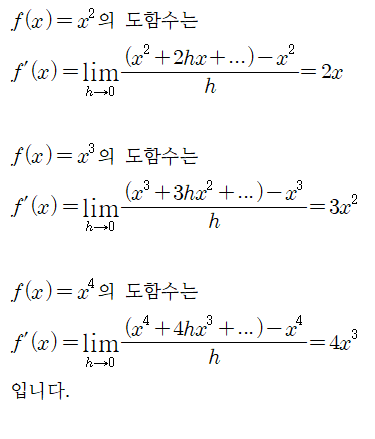
이를 연장하면, f(x)=x^n의 도함수는 f'(x)=nx^(n-1)임을 알 수 있습니다.
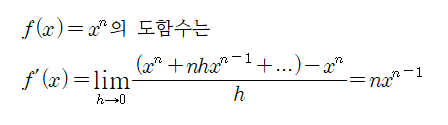
[정리] 다항함수의 미분은 계수와 차수를 곱해 계수로 나타내고, 차수를 1 낮추어 적습니다.
[주의] 상수를 미분하면 0이 됩니다. f(x), f(x+h)에 상관없이 같은 값을 가지기 때문에 사라집니다.
[주의] 일차식을 미분하면 계수만 남습니다.
예)
함수 y=2x+1의 도함수는
2x의 계수가 2, 차수가 1이므로,
2가 되고,
상수 1은 사라집니다.
따라서 y'=2입니다.
예)

* 학습지 미리보기


* 첨부파일
* 닫는 말
이번 학습지는 수학2의 미분 단원 중 도함수를 구하는 학습지입니다. 도함수의 정의를 활용하여 여러 가지 다항함수의 도함수를 구해보세요.
✔ 이 글이 도움이 되셨나요?
- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 고2, 고3, 수학2, 미분, 미분가능한 함수, 미분하는 방법, 다항함수의 미분법, 도함수의 뜻, 도함수 구하기, 도함수 학습지, 문제, 다운, 다운로드, pdf, 학습지제작소
'수학 학습지 > 수학II' 카테고리의 다른 글
| [수학2] 부정적분 (개념+수학문제) | 다항함수의 부정적분 연습문제 (0) | 2022.05.02 |
|---|---|
| [수2] 다항함수의 미분, 도함수의 함숫값 (개념+수학문제) (0) | 2022.02.16 |
| 접선의 기울기와 미분계수, 미분계수의 기하적 의미 (개념+수학문제) (0) | 2021.01.30 |
| 미분계수, 순간변화율 구하기 (개념+수학문제) (0) | 2021.01.25 |
| 평균변화율, 증분 (수학2 개념+수학문제) (0) | 2021.01.15 |

 학습지제작소 관리자
학습지제작소 관리자 2021. 2. 7.
2021. 2. 7. 댓글
댓글
