학습지제작소 관리자
2021. 1. 19.
* 같이 보면 좋은 글
* 나머지에 대한 문제
최대공약수는 과부족에 대한 문제를 해결하는데 사용할 수 있었습니다.
세 수를 어떤 수로 나눌 때 나머지를 준 뒤, 어떤 수를 구하는 문제였습니다.
최소공배수도 마찬가지로 과부족 상황에서 문제를 해결하는 데 사용될 수 있습니다.
이때 어떤 수는 나누어지는 수가 아니라 나누는 수가 됩니다.
[참고] 나누는 수, 나누어지는 수
나눗셈 a÷b=c에서 a를 나누는 수(제수), b를 나누어지는 수(피제수), c를 몫이라고 부릅니다.
만약에 나누어떨어지지 않는다면
a÷b=c...d로 나타낼 수 있고, d는 나머지가 됩니다.
돌아가서, 최대공약수 유형은 '어떤수로 85를 나누면 1이 남고...'상황으로 어떤 수 □에 대한 식으로 나타내면85÷□=☆...1로 나타낼 수 있습니다.
반면 최소공배수 유형은 다음과 같습니다.
[풀이] 어떤 수를 6, 24, 18로 나누면 모두 1이 부족한 상황으로, 어떤 수는 나누는 수입니다.
이때, 어떤 수를 □라고 약속할 때 □에 1을 더해주면 6, 24, 18로 모두 나누어 떨어집니다.
이를 식으로 나타내면,
(□+1)÷6=☆
(□+1)÷24=△
(□+1)÷18=♡
이 됩니다.
즉, (□+1)은 6, 24, 18의 공배수가 되고, 어떤 수로 가능한 수는 6, 24, 18의 최소공배수의 배수입니다.
6, 24, 18의 최소공배수를 소인수분해를 이용하여 구하면
으로, 최소공배수는
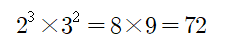
입니다.
따라서 (□+1)로는 72, 144, 216...이 가능하고
어떤 수로는 71, 143, 215...가 가능합니다.
이 중 가장 작은 값은 71이므로
정답은 71입니다.
풀이 과정을 정리하면 다음과 같습니다.
1단계. 어떤 수를 □로 놓고 약수 관계 놓기
(a로 하셔도, x로 하셔도 괜찮습니다. 진도 상 문자와 식 앞의 단원이기 때문에 □로 놓았습니다.)
2단계. 최소공배수 구하기
3단계. 문제에서 구하고자 하는 값 구하기
* 학습지 미리보기
* 첨부파일
* 닫는 말
이번 글은 최대공약수의 활용에 이어서 최소공배수의 활용에 대한 문제입니다.
나머지에 대한 문제가 어렵기 때문에 먼저 문제를 푸는 방법과 학습지를 공유하게 되었습니다.
여러분의 학습 또는 지도에 도움이 되기를 바랍니다.
감사합니다.
✔ 이 글이 도움이 되셨나요?
- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.
- 학습지제작소를 구독하시면 빠르게 소식을 받아보거나 프리미엄 학습지를 신청하실 수 있습니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 중1, 중학교 1학년, 최소공배수의 활용, 최소공배수 나머지, 연습문제, 최소공배수 과부족 학습지, 다운, 다운로드, 학습지제작소
'수학 학습지 > 중학교 1학년 1학기' 카테고리의 다른 글
| 소금물의 농도에 대한 문제 - 일차방정식의 활용 (4) (개념+수학문제) (3) | 2021.02.04 |
|---|---|
| [보충] 정수의 덧셈과 뺄셈 연산연습 50문제 다운로드 (2) | 2021.01.21 |
| 분수에 대한 문제, 자연수가 되게 하는 n의 값 - 최대공약수의 활용 (3) (0) | 2021.01.09 |
| 나머지(과부족)에 대한 문제 - 최대공약수의 활용 (2) (0) | 2020.12.13 |
| [수학I] 시그마를 이용하여 식의 값 구하기 보충 연습문제 50제 (0) | 2020.12.11 |
댓글