학습지제작소 관리자
2020. 12. 6.
* 같이 보면 좋은 글
* 최대공약수의 활용
최대공약수는 생활 속에서 활용할 수 있습니다.
이번 시간에는
분배상황,
직육면체를 만드는 상황,
나무를 심는 상황,
분수가 자연수가 되는 상황
네 가지를 살펴보고
다음 시간에는 나머지가 주어지는 상황을 보고 문제를 해결해봅시다.
* 분배상황 : 똑같이 나누어주는 상황
예) 감자 105개, 당근 63개, 피망 175개를 되도록 많은 사람에게 똑같이 나누어주려고 할 때, 최대 몇 명에게 나누어줄 수 있는지 구하시오.
첫 번째 상황은 최대한 많은 사람들에게 음식 또는 물건을 똑같이 나누어주는 상황입니다.
105, 63, 175를 어떤 수로 나누었을 때 모두 나누어 떨어져야 하므로
105, 63, 175의 최대공약수를 구해야 합니다.
따라서 최대 7명에게 음식을 나누어줄 수 있습니다.
* 정육면체로 직육면체를 만드는 상황
예) 가로의 길이가 12cm, 세로의 길이가 18cm, 높이가 24cm인 직육면체가 있다. 정육면체를 쌓아 같은 모양의 직육면체를 만들려고 할 때, 가능한 정육면체들의 모서리의 길이 중 최댓값을 구하시오.
정육면체로 주어진 직육면체를 만들기 위해서는
정육면체의 모서리의 길이는 직육면체의 길이의 약수이어야 합니다.
졍육면체의 모서리의 길이를 x라고 놓으면
x는 12의 약수
x는 18의 약수
x는 24의 약수입니다.
따라서 x는 12, 18, 24의 공약수입니다.
문제에서는 가능한 정육면체의 모서리의 길이의 최댓값을 물어보았으므로
12, 18, 24의 최대공약수를 구해야 합니다.
따라서 정육면체의 한 모서리의 길이의 최댓값은 6입니다.
[참고] 이를 그림으로 나타내면 다음과 같습니다.
* 나무를 심는 상황 : 직사각형 모양에 같은 간격으로
예) 가로의 길이가 110m, 세로의 길이가 40m인 직사각형 모양의 정원이 있다. 이 정원에 같은 간격으로 나무를 최대한 적게 심으려고 할 때, 나무 사이의 간격을 구하시오. (단, 정원의 꼭짓점에는 반드시 나무를 심는다.)
정원을 그림으로 나타내면 다음과 같습니다.
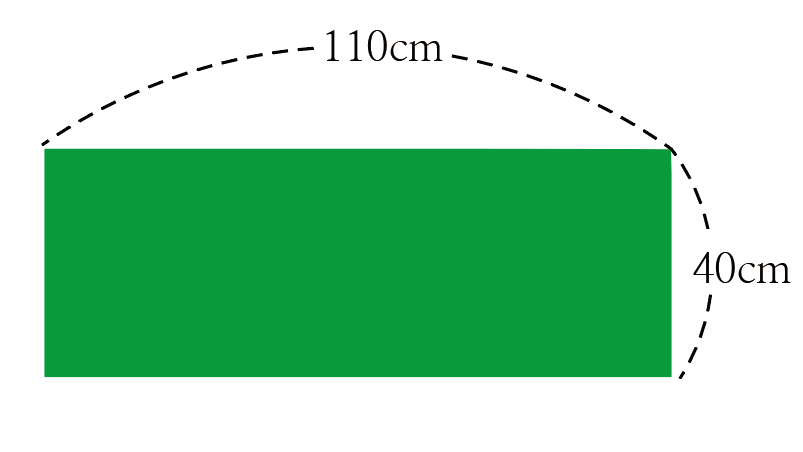
나무 사이의 간격은 항상 같아야 하므로
110과 40의 공약수이어야 합니다.
그리고 최대한 적게 심어야 하므로
최대공약수입니다.
110과 40의 최대공약수를 구하면 10입니다.
따라서 나무 사이의 간격은 10m입니다.
[참고] 정원의 꼭짓점에 반드시 나무를 심는다면 그림과 같이 나타낼 수 있습니다.
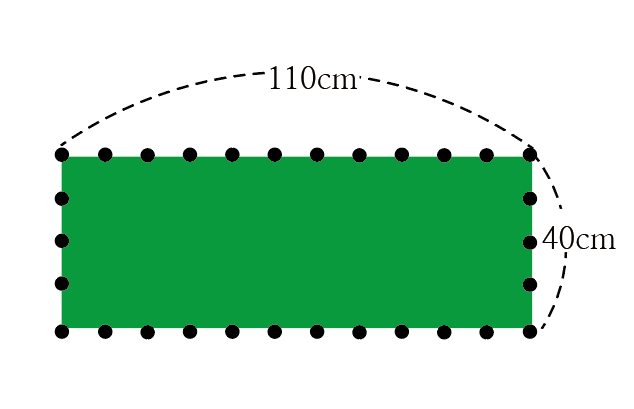
나무(점)의 개수를 세어보면 30개임을 알 수 있습니다.
* 분수가 자연수로 되는 상황
예)
분수가 자연수로 되는 상황은 분모가 미지수로 주어진 상황으로, 두 분자의 공약수를 구해야 합니다.
* 학습지 미리보기
* 첨부파일
[2021-02-23 수정] 나무를 심는 문제의 표현을 일부 수정하였습니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지 제작소에 있으며, 비상업적, 상업적 이용이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 중1, 중학교 1학년, 최대공약수의 활용, 똑같이 나누어줄 때 최대공약수 문제, 쌓기나무 최대공약수 문제, 입체도형 최대공약수, 정육면체, 나무 심기 문제, 똑같은 간격 최대공약수, 분수가 자연수가 되는 문제, pdf, 다운, 다운로드, 학습지제작소
'수학 학습지 > 중학교 1학년 1학기' 카테고리의 다른 글
| 나머지(과부족)에 대한 문제 - 최대공약수의 활용 (2) (0) | 2020.12.13 |
|---|---|
| [수학I] 시그마를 이용하여 식의 값 구하기 보충 연습문제 50제 (0) | 2020.12.11 |
| 도형에 대한 문제 - 일차방정식의 활용 (3) (0) | 2020.12.05 |
| [보충] 유리수의 사칙계산, 혼합계산 (3) : 항3개 ver. (0) | 2020.11.25 |
| 소인수의 합 (개념+수학문제) (0) | 2020.11.15 |
댓글