
| 같이 보면 좋은 글
| 시초선과 동경
(1) 시초선
시초선이란, 원점 O에 대하여 그은 반직선입니다.
시초선은 대체로 좌표평면의 x축 방향(오른쪽 방향)으로 긋습니다.

위 그림에서 시초선은 반직선 OX입니다.
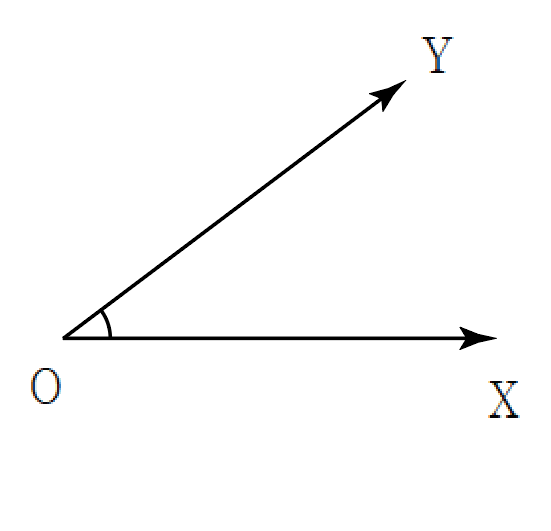
같은 점(O)에서 출발하여 임의의 점 Y와 이은 반직선 OY에 대하여,
각 XOY의 크기는 반직선 OX에서 반시계 방향으로 반직선 OY까지 회전한 정도를 나타냅니다.
[참고] 반시계방향을 양의 방향, 시계방향을 음의 방향이라고 부릅니다.
[참고] 반시계방향은 제1,2,3,4사분면 순서로 놓았을 때 방향과 같습니다.
(2) 동경
동경이란, 반직선 OY와 같이, 각을 이루는 두 반직선 중 시초선이 아닌 반직선을 말합니다.
각의 크기는 곧 시초선이 양의 방향으로 움직였을 때 동경과 겹쳐지는 정도를 말합니다.
| 일반각
(1) 반직선이 한 바퀴를 돌 때의 각
원점이 O인 반직선이 한 바퀴를 돌면 몇도 일까요?

시초선과 동경이 일치할 때 각의 크기는 0º입니다.
사실 동경이 한 바퀴를 돌았을 때 시초선과 동경은 다시 겹쳐집니다.
따라서 이 그림은 0º일 수도 있고 360º일 수도 있습니다.
동경을 음의 방향으로 한 바퀴를 돌면 -360º일 수도 있습니다.

이를 계속 확장하면, n이 정수일 때 360º×n으로 나타낼 수 있습니다.
(2) 일반각의 의미
각 YOX에 대해 0º≤α<360º, n을 정수로 놓으면
360º×n+αº로 표현할 수 있습니다.
이를 일반각이라고 부릅니다.
[정리] 일반각은 360º×n+αº (단, n은 정수, 0º≤α<360º)
[정리] 일반각은 같은 동경이 나타내는 무수히 많은 각을 하나의 식으로 나타낼 수 있다.
[정리] 일반각의 α가 같다면, 동경이 나타내는 위치가 서로 같다.
예) 30º, 390º, -330º, 3630º... -> 360º×n+30º
(3) 예제
* 다음 각의 동경이 나타내는 일반각을 구하시오.
1. 600º
2. -500º
3. 110º
4. 1090º
<해설>
1. 600을 360으로 나누면,
몫이 1, 나머지가 240
따라서 360º×n+240º
2. -500을 360으로 나누면,
몫이 -2, 나머지가 220
따라서 360º×n+220º
3. 110을 360으로 나누면,
몫이 0, 나머지가 110
따라서 360º×n+110º
3. 1090을 360으로 나누면,
몫이 3, 나머지가 10
따라서 360º×n+10º
| 학습지 미리보기


| 첨부파일
| 닫는 말
삼각함수 단원은 처음부터 중학교까지는 주로 180º까지 나타내었다가 음수인 각과 360보다 큰 각을 다루게 되어 낮설 수 있습니다.
일반각은 정수 n에 대하여 동경의 위치를 나타낸 식입니다.
n과 α의 의미는 뒷 부분을 학습할 때 중요한 기초가 되니,
문제를 풀어보면서 일반각을 나타내는 연습을 해보세요.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지 제작소에 있으며, 비상업적, 상업적 이용이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 일반각, 동경, 시초선, 일반각 나타내는 법, 일반각 문제, 시계 방향, 반시계 방향, 동경의 위치, 고2, 수학1, 수학I, 삼각함수, 동경의 뜻, 일반각의 뜻, 시초선의 뜻, 일반각 연습문제, 무료, 다운, pdf, 학습지제작소
'수학 학습지 > 수학I' 카테고리의 다른 글
| [수학I] 14. 삼각함수의 뜻, 사인(sin) 코사인(cos) 탄젠트(tan) 값 구하는 방법 (개념+수학문제) (0) | 2020.08.06 |
|---|---|
| [수학I] 13. 호도법과 육십분법, 라디안 연산연습 (개념+수학문제) (0) | 2020.08.05 |
| [수학I] 11. 로그방정식, 로그 미지수 값 구하는 법 (개념+수학문제) (0) | 2020.07.29 |
| [수학I] 10. 로그함수의 그래프, 정의역, 점근선, 평행이동, 대칭이동 (개념+수학문제) (0) | 2020.07.17 |
| [수학I] 9. 지수부등식의 의미, 해, 풀이 (개념+수학문제) (0) | 2020.07.16 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 8. 2.
2020. 8. 2. 댓글
댓글
