
* 같이 보면 좋은 글
* 다각형
다각형이란, 여러 개의 선분으로 둘러싸인 도형을 말합니다.
이때 다각형의 선분의 개수에 따라 삼각형, 사각형, 오각형, 육각형...이라고 부릅니다.
예) 선분의 개수가 3개인 다각형: 삼각형
예) 선분의 개수가 7개인 다각형: 칠각형
[개념] 다각형과 다각형이 아닌 것

▶ 왼쪽 하늘색 상자 안의 도형은 모두 다각형입니다. 각각 4개, 5개, 8개의 선분으로 둘러싸여 있습니다.
▶ 오른쪽 노란색 상자 안의 도형은 다각형이 아닙니다.
- 왼쪽 도형(원)은 선분으로 둘러싸여있지 않습니다.
- 오른쪽 도형은 선분으로 둘러싸여있지 않고 끊어져 있습니다.
* 다각형의 대각선 개수
[개념] 다각형의 한 꼭짓점에서 그을 수 있는 대각선 개수
다각형에 따라 한 꼭짓점에서 그을 수 있는 대각선의 개수는 다음과 같습니다. 출발점과 이웃한 두 점을 제외하므로 변의 개수보다 3만큼 작습니다.
| 삼각형 | 없음 |
| 사각형 | 1개 |
| 오각형 | 2개 |
| 육각형 | 3개 |
| (...) | (...) |
| $n$각형 | $(n-3)$개 |
예) 십각형의 한 꼭짓점에서 그을 수 있는 대각선 개수: $7$개
예) 이십각형의 한 꼭짓점에서 그을 수 있는 대각선 개수: $17$개

그림과 같이 오각형 ABCDE가 있습니다. 대각선은 모두 몇 개일까요?
점 A에서 그을 수 있는 대각선은 선분 AC, AD로 모두 2개입니다.
점 B에서 그을 수 있는 대각선은 선분 BD, BE로 모두 2개입니다.
점 C에서 그을 수 있는 대각선은 선분 CA, CE로 모두 2개입니다.
점 D에서 그을 수 있는 대각선은 선분 DA, DB로 모두 2개입니다.
점 E에서 그을 수 있는 대각선은 선분 EB, EC로 모두 2개입니다.
그런데 선분 AC와 CA, 선분 AD와 DA와 같이 선분이 2개씩 겹칩니다.
따라서 2로 나누면 오각형의 대각선 개수는
$\cfrac{5 \times 2 } {2} = 5$(개)가 됩니다.
[개념] 다각형의 대각선 개수
다각형의 대각선 개수는 다음과 같이 구할 수 있습니다.
| 다각형 | 변의 개수(개) | 한 점에서 그을 수 있는 대각선의 개수(개) | 대각선의 개수(개) |
| 사각형 | $4$ | $1$ | $\cfrac{4 \times 1 } {2} = 2$ |
| 오각형 | $5$ | $2$ | $\cfrac{5 \times 2 } {2} = 5$ |
| 육각형 | $6$ | $3$ | $\cfrac{6 \times 3 } {2} = 9$ |
| 칠각형 | $7$ | $4$ | $\cfrac{7 \times 4 } {2} = 14$ |
| 팔각형 | $8$ | $5$ | $\cfrac{8 \times 5 } {2} = 20$ |
| 구각형 | $9$ | $6$ | $\cfrac{9 \times 6 } {2} = 27$ |
| 십각형 | $10$ | $7$ | $\cfrac{10 \times 7 } {2} = 35$ |
| (...) | |||
| $n$각형 | $n$ | $n-3$ | $\cfrac{n \times (n-3) } {2} $ |
* 정다각형의 내각, 외각
[개념] 정다각형: 정다각형이란, 변의 길이가 서로 같고 내각의 크기가 서로 같은 다각형을 말합니다.
예) 정삼각형, 정사각형, 정오각형
[개념] 정다각형의 내각의 크기
정다각형의 내각의 크기는 한 꼭짓점에서 대각선을 그어 구할 수 있습니다.
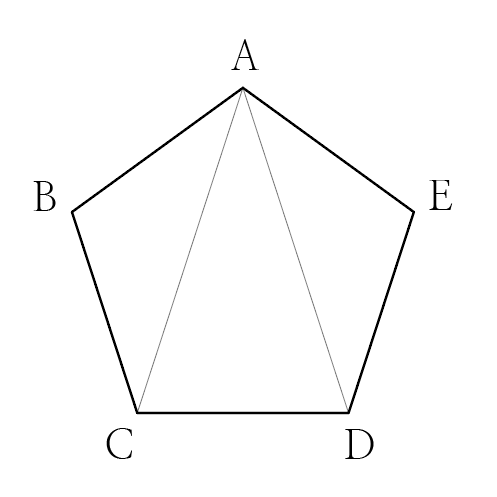
그림과 같이 정오각형 ABCDE의 꼭짓점 A에서 두 대각선을 그으면 3개의 삼각형이 만들어집니다.
따라서 5개의 내각의 크기의 합은 삼각형 3개의 내각의 합과 같습니다.
삼각형 3개의 내각의 합은 $180° \times 3 = 540°$입니다.
이처럼 다각형의 내각의 합은 다음과 같은 규칙이 있습니다.
| 다각형 | 삼각형 | 사각형 | 오각형 | 육각형 | (...) | $n$각형 |
| 내각의 합(°) | 180 | 360 | 540 | 720 | (...) | $180 \times (n-2)$ |
한 내각의 크기는 내각의 합을 꼭짓점의 개수로 나누면 되므로 다음과 같습니다.
| 다각형 | 삼각형 | 사각형 | 오각형 | 육각형 | (...) | $n$각형 |
| 내각의 합(°) | 180 | 360 | 540 | 720 | (...) | $180 \times (n-2)$ |
| 꼭짓점(개) | 3 | 4 | 5 | 6 | (...) | $n$ |
| 한 내각의 크기(°) | 60 | 90 | 108 | 120 | (...) | $\cfrac{180 \times (n-2)}{n}$ |
[개념] 정다각형의 외각의 크기
정다각형의 외각의 합은 항상 360°입니다.
까닭) 정다각형의 외각과 내각의 크기를 모두 더하면 $180 n°$입니다. 여기에서 내각의 합인 $180 \times (n-2)°$를 빼면 항상 $360°$가 남습니다.
이러한 이유로 정n각형의 한 외각의 크기는 $( \cfrac{360}{n} )°$입니다. 정다각형의 외각의 크기는 서로 같기 때문입니다.
| 다각형 | 삼각형 | 사각형 | 오각형 | 육각형 | (...) | $n$각형 |
| 외각의 합(°) | 360 | 360 | 360 | 360 | (...) | 360 |
| 꼭짓점(개) | 3 | 4 | 5 | 6 | (...) | $n$ |
| 한 외각의 크기(°) | 120 | 90 | 72 | 60 | (...) | $\cfrac{360}{n}$ |
* 학습지 미리보기

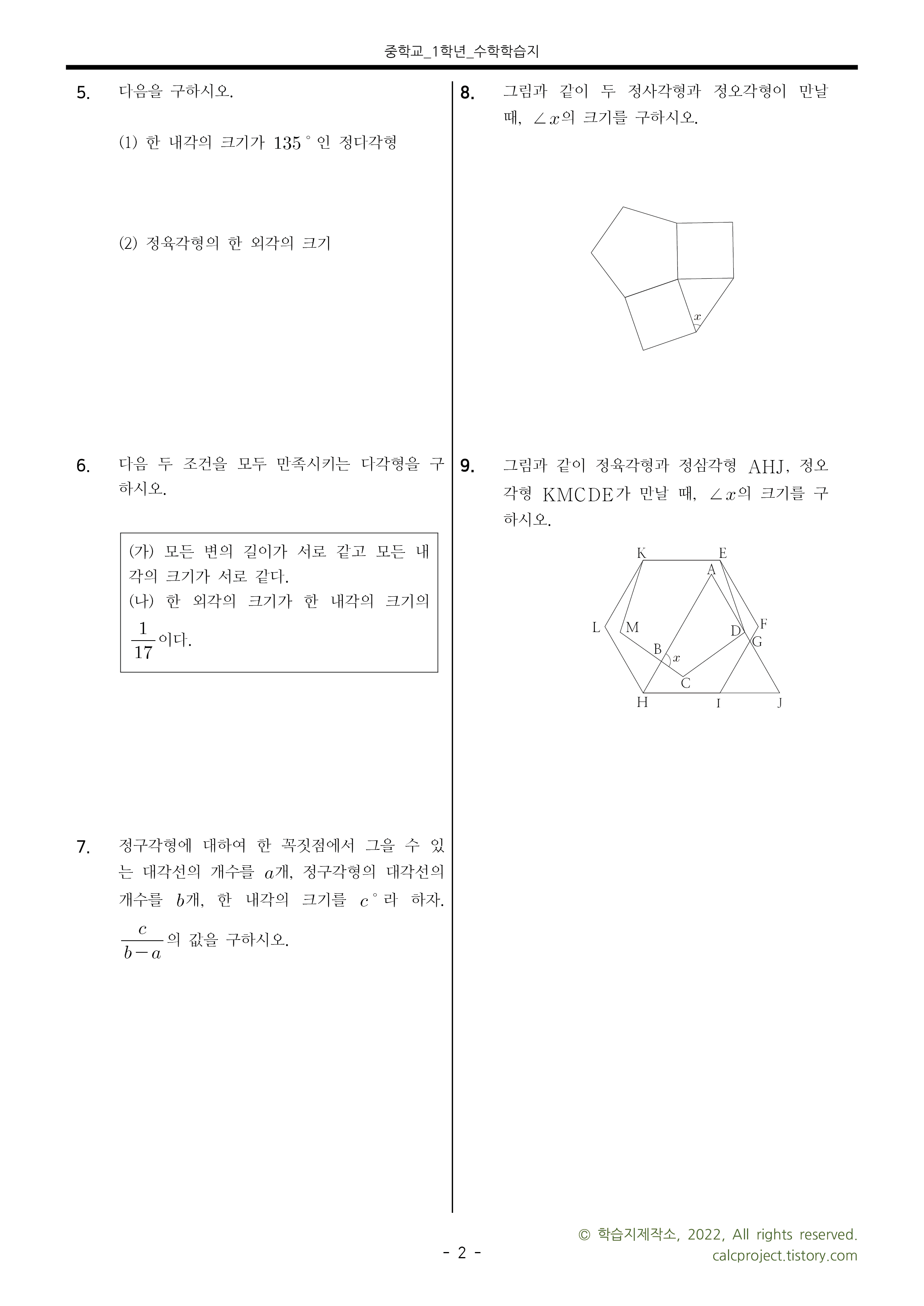
* 첨부파일
* 닫는 말
이번 시간에는 평면도형 단원의 다각형을 살펴보았습니다. 새로운 개념과 공식이 나와 어려운 내용입니다. 공식을 단순히 외우기보다는 사례를 바탕으로 공식을 이해해보세요.
✔ 이 글이 도움이 되셨나요?
- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 도형 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.
- 다른 사진을 참조한 경우, 파일 마지막 페이지에 출처를 밝히고 있습니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2022. 학습지제작소. All Rights Reserved.
#태그 : 중1, 중학교 1학년, 평면도형, 다각형, 다각형의 조건, 다각형 대각선의 개수, 다각형의 대각선, 다각형의 내각의 합, 정다각형의 내각의 크기, 정다각형의 외각
'수학 학습지 > 중학교 1학년 2학기' 카테고리의 다른 글
| [중1-2] 부채꼴의 넓이 공식, 부채꼴 둘레 구하기 (개념+수학문제) (0) | 2022.09.28 |
|---|---|
| [중1-2] 원의 둘레(원주), 넓이 (개념+수학문제) | 중학교 1학년 2학기 수학학습지 PDF (0) | 2022.09.17 |
| [중1-2] 동위각, 엇각, 두 직선이 평행할 조건 (개념+수학문제) (0) | 2022.07.28 |
| [중1-2] 기본도형 > 각, 맞꼭지각, 점과 직선 사이의 거리 (개념+수학문제) (0) | 2022.07.17 |
| [중1-2] 기본도형 > 점, 선, 면의 이해 | 교점, 교선, 중점 수학학습지 (개념+수학문제) (1) | 2022.06.25 |

 학습지제작소 관리자
학습지제작소 관리자 2022. 8. 17.
2022. 8. 17. 댓글
댓글
