곱셈은 인류 문명 발전에 핵심적인 역할을 수행했습니다.
보다 효율적으로 계산할 수 있게 도와주었기 때문입니다.
그렇다면 곱셈의 의미는 무엇일까요?
우리는
3×2=6
11×4=44
12×12=144
임을 배웠고, 이를 일상생활에서 사용하고 있습니다.
그런데 곱셈의 의미가 구체적으로 무엇인지 생각해보기가 쉽지 않습니다.
이번 시간에는 곱셈의 세 가지 의미로 동수누가, 배의 개념, 곱집합을 알아보겠습니다.
1. 동수누가
동수누가(同數累加)란 같은 수를 여러 번 더하는 상황을 말합니다.
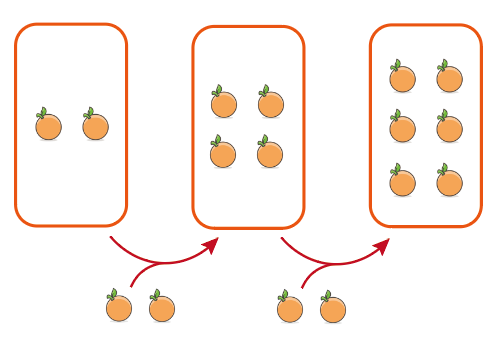
그림의 왼쪽, 가운데, 오른쪽에는 각각 2개, 4개, 6개의 오렌지가 있습니다.
그리고 2개에서 2개의 오렌지를 더해 4개의 오렌지가,
4개의 오렌지에서 2개의 오렌지를 더해 6개의 오렌지가 되었습니다.
4는 2를 두 번 더한 것과 같고
6은 2를 세 번 더한 것과 같습니다.
4=2+2
6=2+2+2
로 나타낼 수 있습니다.
이와 같이 같은 수를 여러 번 더하는 상황을 동수누가 상황이라고 부릅니다.
[참고] 페아노(Peano)는 이 아이디어에서 곱셈을 정의합니다.
페아노 공리
이 약속에 따르면 2×1=2, 2×2=4, 2×3=6, 2×4=8, 2×5=10...
를 정의할 수 있습니다.
2. 배의 개념
곱은 묶음의 개념으로 생각해볼 수도 있습니다.
묶음의 개수를 '배'라고 부릅니다.

왼쪽 상자에는 오렌지가 2개씩 1묶음이 있습니다.
가운데 상자에는 오렌지가 2개씩 2묶음이 있습니다.
오른쪽 상자에는 오렌지가 2개씩 3묶음이 있습니다.
2의 1배는 2
2의 2배는 4
2의 3배는 6입니다.
3. 곱집합의 개념
조금 어렵지만, 곱셈은 곱집합으로 생각해볼 수 있습니다.
집합 A, B에 대하여
곱집합 A×B={(a,b)|a∈A, b∈B}이 성립합니다.
다시 말해, A에서 하나의 원소, B에서 하나의 원소를 짝지은 순서쌍을 원소로 가지는 집합이 곱집합입니다.
예) 수민이의 옷장에는 스웨터, 티셔츠, 와이셔츠가 있습니다. 신발장에는 운동화, 구두가 있습니다. 수민이가 옷과 신발을 하나씩 고르는 경우는 모두 몇 가지입니까?
옷장에 걸려있는 옷을 집합 A
신발장에 높여있는 신발을 집합 B라고 놓으면,
A={스웨터, 티셔츠, 와이셔츠}
B={운동화, 구두}
로 생각할 수 있습니다.
이때 옷 한 벌과 신발 한 짝을 고르는 방법은 다음과 같습니다.
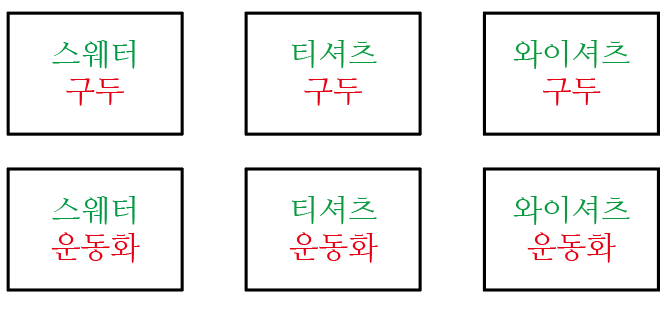
(스웨터, 구두) (티셔츠, 구두) (와이셔츠, 구두)
(스웨터, 운동화) (티셔츠, 운동화) (와이셔츠, 운동화)
모두 여섯 가지입니다.
이때, 집합 A의 원소의 개수는 3개
집합 B의 원소의 개수는 2개입니다.곱집합 A×B의 원소의 개수는 6개입니다.
[정리] 곱집합의 원소의 개수
집합 A,B에 대하여 n(A×B)=n(A)×n(B)
곱집합의 개념은 곱셈의 교환법칙을 쉽게 설명할 수 있습니다.
곱셈의 교환법칙: a×b=b×a
동수누가와 배의 개념으로는 곱셈의 교환법칙을 직관적으로 이해하기 어렵습니다.
예를 들어, 2+2+2=3+3임을 이해하기 위해서는 계산해보거나 조작 활동이 필요합니다.
2의 3배, 3의 2배도 마찬가지입니다.
그러나 곱집합은 곱셈의 교환법칙을 이해하기 적절합니다.
두 문제 상황을 비교해봅시다.
예) 수민이의 옷장에는 스웨터, 티셔츠, 와이셔츠가 있습니다. 신발장에는 운동화, 구두가 있습니다. 수민이가 옷과 신발을 하나씩 고르는 경우는 모두 몇 가지입니까?
예) 수민이의 옷장에는 스웨터, 티셔츠, 와이셔츠가 있습니다. 신발장에는 운동화, 구두가 있습니다. 수민이가 신발과 옷을 하나씩 고르는 경우는 모두 몇 가지입니까?
옷과 신발을 고르나, 신발과 옷을 고르나 두 상황은 같은 상황입니다.
옷 한 벌을 고르는 경우는 3가지,
신발 한 짝을 고르는 경우는 2가지로,
3×2=2×3임을 쉽게 얻을 수 있습니다.
지금까지 곱셈의 세 가지 의미를 알아보았습니다.
당연하게 생각했던 곱셈이 이렇게 다양한 상황으로 바라볼 수 있음이 신기합니다.
'글의 세 가지 의미-동수누가, 배, 곱집합' 글은 여기서 마치겠습니다.
감사합니다.
'교육 소식 > 교과서 용어 정리' 카테고리의 다른 글
| 막대그래프와 히스토그램 (0) | 2022.07.23 |
|---|---|
| 관용 표현 (0) | 2021.09.01 |
| 외연량과 내포량 (0) | 2021.08.22 |
| [중3] 일차함수의 기울기와 tan(탄젠트)의 관계 (0) | 2021.08.14 |
| 수학적 확률과 통계적 확률 (0) | 2021.08.01 |

 학습지제작소 관리자
학습지제작소 관리자 2021. 8. 16.
2021. 8. 16. 댓글
댓글
