[2021-02-18 수정/2022-04-08 수정] Day 1 답지 부분에 오류가 있어 수정 후 다시 올렸습니다.
[2021-10-30수정] <중괄호의 의미>항 설명을 수정하였습니다.
안녕하세요, 학습지제작소입니다.
지난 포스팅에서는 괄호가 없는 일차방정식과, 소괄호가 있는 일차방정식에 대해 공부했는데요,
오늘은 중괄호가 있는 일차방정식을 풀어보려고 합니다.
| 중괄호의 의미
원래 혼합계산에서 괄호는 소괄호() -> 중괄호{} -> 대괄호[] 로 푸는데요, 한국에서 이러한 순서로 풀지, 대괄호와 중괄호의 순서에 대한 세계적인 규약은 없다고 합니다. 하지만, 한국 교육과정에서는 소괄호, 중괄호, 대괄호 순서로 풀도록 하고 있으니 이를 따라야겠죠?
중괄호는 소괄호를 푼 다음에 우선순위에 두어야 할 기호로, 중괄호를 풀고 난 후, 곱셈 나눗셈 계산을 하도록 합니다.
예를 들어보겠습니다.

위 문제는 오늘 업로드하는 학습지의 첫번째 문제인데요, 소괄호와 중괄호가 모두 있는 일차방정식입니다.
<풀이>
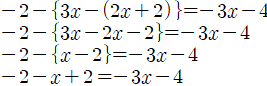
중괄호가 있는 일차방정식을 풀기 위해서는
1. 분배법칙을 이용해 소괄호를 푼 후,
2. 동류항끼리 계산해야합니다.
3. 분배법칙을 이용해 중괄호를 푼 후,

4. 동류항끼리 계산합니다.
5. 이항하여 왼쪽에는 일차식, 오른쪽에는 상수항을 구합니다.
6. 양변을 2로 나누어 해를 구합니다.
중괄호가 있는 식은 분배법칙을 여러 번 하고, 동류항을 여러 번 계산해야하기 때문에 과정이 상당히 긴 편입니다. 이번 학습지에서는 이러한 유형을 여러 문제 만나면서 해결해보는 시간을 가질 수 있을 것으로 기대합니다.
| 중괄호가 있는 일차방정식을 푸는 순서
위 예제에서 살펴보았듯이, 중괄호가 있는 일차방정식은 다음과 같은 순서로 풉니다.
1. 분배법칙을 이용해 소괄호를 푼 후,
2. 동류항끼리 계산해야합니다.
3. 분배법칙을 이용해 중괄호를 푼 후,
4. 동류항끼리 계산합니다.
5. 이항하여 왼쪽에는 일차식, 오른쪽에는 상수항을 구합니다.
6. 양변을 2로 나누어 해를 구합니다.
| 예제
1.
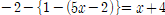
2.
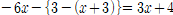
<풀이>
1.
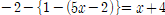
중괄호를 풀면, 5x-2에 -1이 분배되어 -5x+2가 됩니다.
-5x+2앞에 1이 있으므로 동류항 2와 1을 더하여
-5x+3을 얻습니다.
-5x+3앞에 -1이 묶여 있으므로 -1을 분배합니다. 따라서 5x-3을 얻을 수 있습니다.
그 앞에 -2가 더해져 있으므로 동류항 -3과 -2를 더해 5x-5를 얻습니다.
5x-5=x+4이고, 이항하면
4x=9
x = 9/4
2.
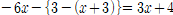
중괄호를 풀면, x+3에 -1이 분배되어 -x-3이 됩니다.
-x-3앞에 3이 있으므로 동류항 -3와 3을 더하여
-x를 얻습니다.
-x앞에 -1이 묶여 있으므로 -1을 분배합니다. 따라서 x를 얻을 수 있습니다.
그 앞에 -6x가 더해져 있으므로 동류항 -6x와 x를 더해 -5x를 얻습니다.
-5x=3x+4이고, 이항하면
-8x=4
x = - 1/2
| 일차방정식을 잘 풀기 위해서는...
1. 미지수 x의 의미를 알고 있어야 합니다.
미지수 x란 알 수 없는 수로, x값에 따라 방정식이 참이 되기도, 거짓이 되기도 합니다.
이 중 방정식이 참이 되게 하는 x의 값을 우리는 해라고 합니다.
일차방정식을 푼다는 의미는 해를 구하는 과정이고, 등식을 성립시키는 x의 값을 찾는 것임을 알야야합니다.
2. 등식의 성질을 적극적으로 활용해야 합니다.
방정식은 등식의 일종이기 때문에 등식의 성질이 성립합니다.
이전 포스팅에서 등식의 성질에 대해 잠시 다루었었는데요, 등식의 성질은 이하 네 가지입니다.

0인 경우 나눌 수 없다를 제외하면, 같은 수를 더하거나 빼거나 곱하거나 나눌 수 있습니다. 이를 자유자재로 활용하여 좌항을 x만 남겨야겠죠?
3. 교환법칙, 결합법칙, 분배법칙을 사용해야합니다.
'어찌보면 당연한거 아닌가요?'하고 넘어간 교환법칙, 결합법칙은
문자가 들어간 식에서 중요한 역할을 합니다.
물론, 유리수의 사칙연산에서는 교환법칙과 결합법칙이 무의식적으로 쓰일 수 있습니다.
예를 들어,
식 (-11)+(+2)+(+11)에서는 -11과 +11이 눈에 들어오기 때문에 2라는 값을 생각해낼 수 있습니다.
마찬가지로, 문자가 들어 있는 식에서는 교환법칙과 결합법칙을 떠올리면 효과적인데요,
3x+2-3x+4인 경우, 교환법칙으로 3x-3x+2+4를 만들어 6을 얻을 수 있습니다.
분배법칙은 괄호가 묶여 있는 식에서 사용해야 하는 법칙으로,
2(a+b)=2a+2b와 같이, 괄호 앞에 있는 상수를 괄호 안의 항에 분배하여 곱하는 내용이었습니다.


오늘은 중괄호가 있는 일차방정식에 대해 포스팅해보았는데요, 이번 학습지를 풀어보면서(지도해보면서) 교환/결합/분배법칙을 연습할 수 있기를 바랍니다.
오늘도 즐거운 하루 보내시기를 바랍니다~
이상 학습지제작소였습니다.
#태그 : 일차방정식, 괄호, 중괄호, 소괄호, 중학교 1학년, 중1 수학, 중학교 1학년 1학기 수학, 일차방정식의 풀이, 일차방정식 문제, 일차방정식 연습문제, 다운, 다운로드, pdf, 수학문제, 괄호가 있는 일차방정식의 풀이, 교환법칙, 결합법칙, 분배법칙
'수학 학습지 > 중학교 1학년 1학기' 카테고리의 다른 글
| 문자와 식 : 식의 값 구하기 (개념+수학문제) (0) | 2020.03.08 |
|---|---|
| 문자로 곱셈식과 나눗셈식 간단히 나타내기 (개념+수학문제) (3) | 2020.03.04 |
| 일차방정식의 뜻과 풀이 (개념+수학문제) (3) | 2020.02.24 |
| 절댓값이 포함된 유리수의 사칙연산 100문제 (2) | 2020.02.02 |
| 정수와 유리수 > 정수의 사칙연산 (0) | 2020.01.29 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 2. 25.
2020. 2. 25. 댓글
댓글
