
| 같이 보면 좋은 글
| 두 직선의 평행 조건
[정리] 두 직선 사이의 관계 (1) : 평행할 조건
두 직선 ax+by+c=0, a'x+b'y+c'=0에 대하여 두 직선이 평행할 조건은
a:a' = b:b' ≠ c:c'
이를 분수로 나타내면,
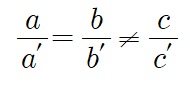
입니다.
예) 두 직선 x+2y+3=0과 3x+6y+10=0은
3÷1, 6÷2는 모두 3으로 같지만
10÷3은 3이 아니므로 두 직선은 평행합니다.
따라서 두 직선은 평행합니다.
예) 두 직선 4x-2y+1=0과 8x-4y+2=0은
4÷8, (-2)÷(-4), 1÷2 모두 1/2로
모두 같습니다.
따라서 두 직선은 평행하지 않습니다.
| 두 직선의 수직 조건
[정리] 두 직선 사이의 관계 (2) : 수직할 조건
두 직선 ax+by+c=0, a'x+b'y+c'=0에 대하여 두 직선이 수직일 조건은
aa'+b'b=0
[증명]
기울기가 m, m'인 두 직선
y=mx+c, y=m'x+c'에 대하여
두 직선이 수직이라면
기울기의 곱은 -1입니다.
그런데 두 직선을 방정식으로 나타내면
mx-y+c=0, m'x-y+c'=0입니다.
x계수의 곱 : m×m' = -1
y계수의 곱 : (-1)×(-1) = 1
따라서 mm'+1=0입니다.
예) 두 직선 x+y-1=0과 x-y+3=0에 대하여
a=1, a'=1, b=1, b'=-1
aa' = 1×1 = 1bb' = 1×(-1) = -1
aa'+bb' = 1+(-1)=0
따라서 두 직선은 수직입니다.
예) 두 직선 3x-2y+10=0, 2x-3y+4=0에 대하여
a=3, b=-2, a'=2, b'=-3
aa' = 6
bb' = 6
aa'+bb' = 6+6 = 12
따라서 두 직선은 수직이 아닙니다.
| 학습지 미리보기


| 첨부파일
| 닫는 말
이번 학습지는 하나의 점을 지나고 어떤 직선에 수직하거나 평행한 직선의 방정식을 구하는 문제로 구성했습니다. 두 직선이 평행할 조건과 수직할 조건을 이해하고, 적용해봅시다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지 제작소에 있으며, 비상업적, 상업적 이용이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 고등수학(상), 고1, 고등학교 1학년, 두 직선 사이의 관계, 두 직선이 평행할 조건, 두 직선이 수직할 조건, 두 직선 사이의 관계 연습문제, 다운, 다운로드, pdf, 학습지제작소
'수학 학습지 > 공통수학1' 카테고리의 다른 글
| 원의 방정식 (개념+수학문제) (0) | 2020.09.04 |
|---|---|
| 점과 직선 사이의 거리 (개념+수학문제) (0) | 2020.08.29 |
| 직선의 방정식 (고등수학 (상) 개념+수학문제) (2) | 2020.08.23 |
| 삼각형의 무게중심 의미, 좌표 구하기 (개념+수학문제) (0) | 2020.08.20 |
| 내분점과 외분점 (개념+공식+수학문제) (0) | 2020.08.19 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 8. 28.
2020. 8. 28. 댓글
댓글
