학습지제작소 관리자
2020. 7. 25.
| 같이 보면 좋은 글
<교과서 목차>
* 각도기 그림은 pixabay.com에서 사용했습니다.
| 개요
각은 한 점에서 시작하는 두 반직선이 이루는 도형입니다.
각은 크기를 가지며, 각의 크기는 서로 비교할 수 있습니다.
2단원 '각도' 단원에서는 각의 크기를 각도라고 부르고, 단위(°)를 이용하게 됩니다.
각도기를 사용하여 각도를 재보거나, 알맞은 각도를 가지는 각을 그리거나,
각을 더하거나 빼는 활동을 합니다.
각도 단원에서 배우는 내용은 다음과 같습니다.
1. 각도의 의미와 단위
2. 각도의 측정과 비교
3. 각도의 어림과 계산
4. 삼각형과 사각형의 각 크기의 합
| 1. 각도의 의미와 단위
(1) 각의 크기 비교하기
가와 나 중에 어떤 각이 더 큰가요?
가는 나보다 더 많이 벌어져 있습니다.
수학에서는 각이 많이 벌어져 있을수록 각이 크다고 이야기합니다.
따라서 각 가는 각 나보다 크기가 더 큽니다.
(2) 각도의 의미와 단위
각도는 각의 크기를 의미합니다.
직각을 90으로 똑같이 나눈 각의 크기를 1°라고 쓰고,1도라고 읽습니다.
각의 크기는 각도기를 이용해 잴 수 있습니다.
각도기는 10개의 눈금마다 숫자가 표시되어 있고, 0부터 180까지의 숫자가 적혀 있습니다.
다섯 눈금마다 굵은 눈금이 표시되어있고,
한 눈금은 1°를 의미합니다.
교과서에서 사용하는 각도기는 안쪽 방향에 오른쪽에서 왼쪽 방향으로도 숫자가 적혀 있습니다.
| 2. 각도의 측정과 비교
(1) 각도의 측정
[정리] 각도기를 이용해 각도를 측정하는 방법은 다음과 같습니다.
1. 각의 꼭짓점에 각도기 중앙 부분과 맞춘다.
2. 각의 한 변과 각도기의 밑금을 맞춘다.
3. 밑금과 맞춘 변이 0 눈금을 가리키는 부분이 바깥쪽 눈금인지 안쪽 눈금인지 살펴본다.
4. 3번에서 찾은 눈금에서 나머지 변과 만나는 눈금을 읽는다.
[정리] 각도기를 이용해 각을 그리는 방법은 다음과 같습니다.
1. 선분을 그린다.
2. 선분의 끝이 각도기의 밑금과 겹치게 한다.
3. 각의 크기에 알맞은 눈금에 점을 찍는다.
4. 각도기의 중앙과 겹쳐있던 선분의 끝과 3번에서 찍은 점을 잇는다.
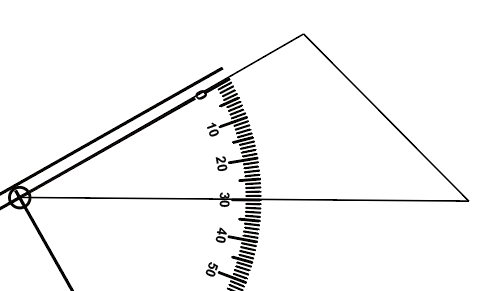
[각도기로 각도의 크기 재어보기]
파란색 각의 크기가 얼마인지 재어봅시다.
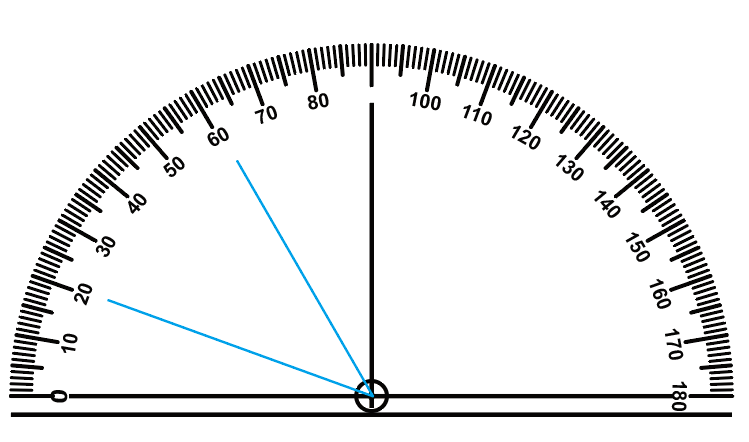
1. 각의 꼭짓점에 각도기 중앙 부분과 맞춘다.
2. 각의 한 변과 각도기의 밑 금을 맞춘다.
3. 밑금과 맞춘 변이 0 눈금을 가리키는 부분이 바깥쪽 눈금인지 안쪽 눈금인지 살펴본다.
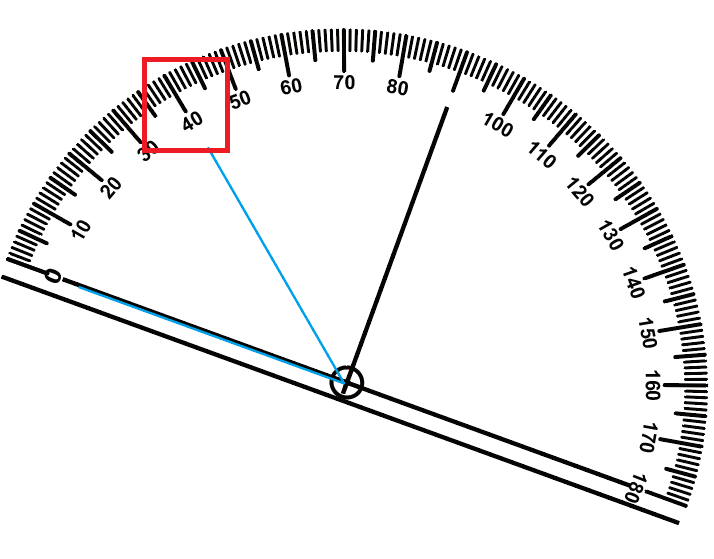
4. 3번에서 찾은 눈금에서 나머지 변과 만나는 눈금을 읽는다. (40°)
(2) 각도의 비교
[정리] 각의 크기를 비교하는 방법
1. 각도기로 각을 재어 각의 크기를 구합니다.
2. 각도기가 가리키는 숫자가 클수록 각의 크기는 큽니다.
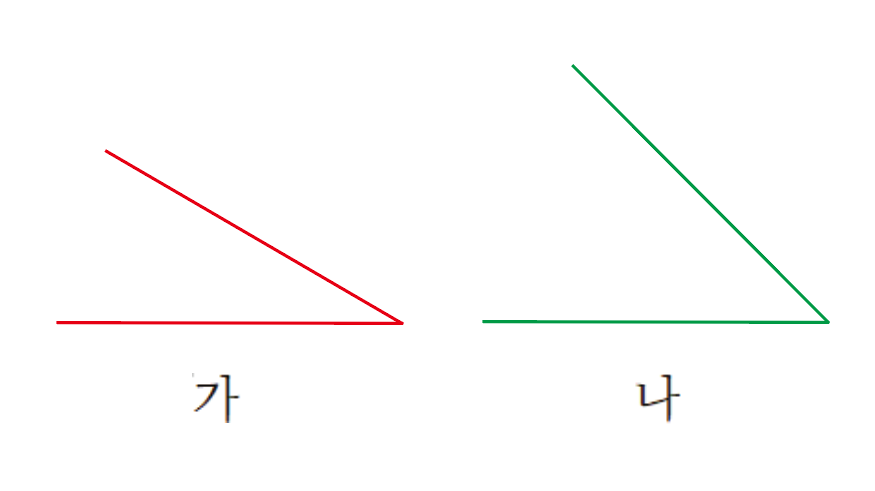
각 가와 나 중 어떤 각의 크기가 더 클까요?
두 각의 크기를 재어보면 다음과 같습니다.
각 가의 크기는 30도입니다.
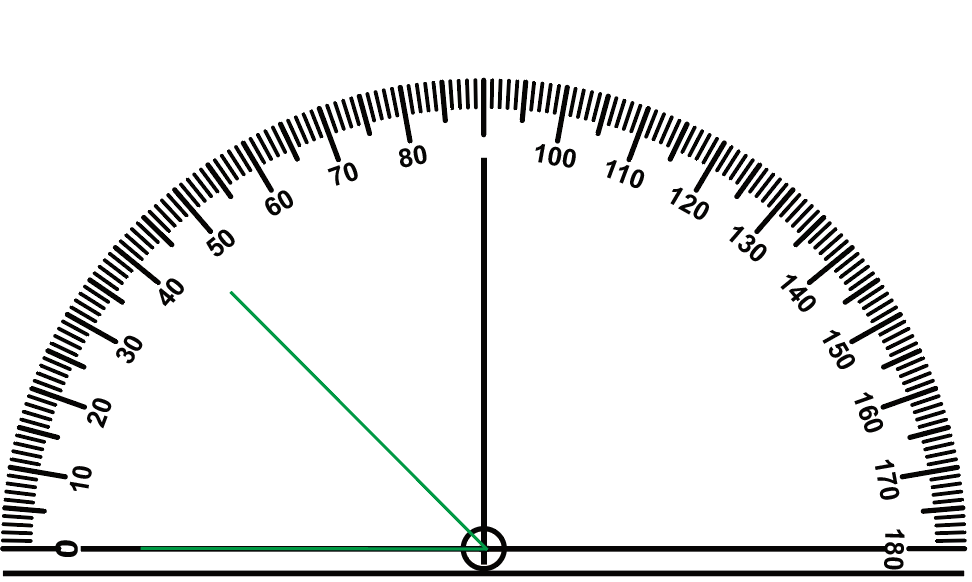
각 나의 크기는 45도입니다.
45가 30보다 크므로
각 나가 각 가보다 더 큽니다.
| 3. 각도의 어림과 계산
(1) 어림하기
각이 주어지면 각의 크기를 어림해볼 수 있습니다.
이때 삼각자의 직각을 사용하면 90보다 큰지 작은지 알 수 있어 어림에 도움이 됩니다.
(2) 각의 합
각의 크기는 더하고 뺄 수 있습니다.
각의 꼭짓점이 같고 한 변이 이어 겹치면 각의 합을 구할 수 있습니다.
각 가와 나의 크기의 합을 구해봅시다.
꼭짓점과 한 변이 겹치게 하면,
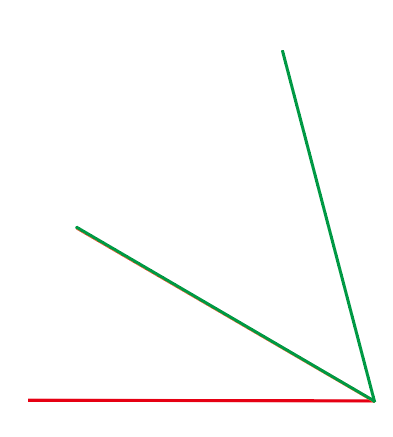
입니다. 각 가와 각 나의 크기는 각각 30도, 45도 입니다.
그렇다면 두 각을 겹친 각의 크기를 구해봅시다.
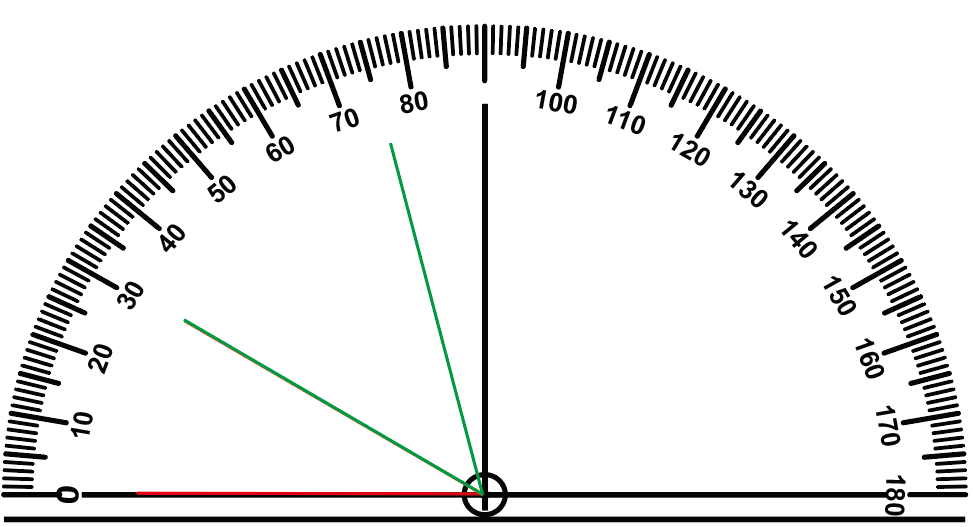
겹친 각의 크기는 75도로, 두 각의 크기의 합과 같습니다.
30°+45°=75°
(3) 각의 차
두 각의 변이 겹치고 포개어지면 각의 차를 구할 수 있습니다.
각 가와 각 나의 차는
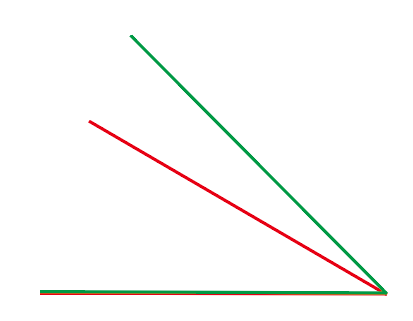
두 각을 겹친 도형의 윗 부분의 각의 크기입니다.
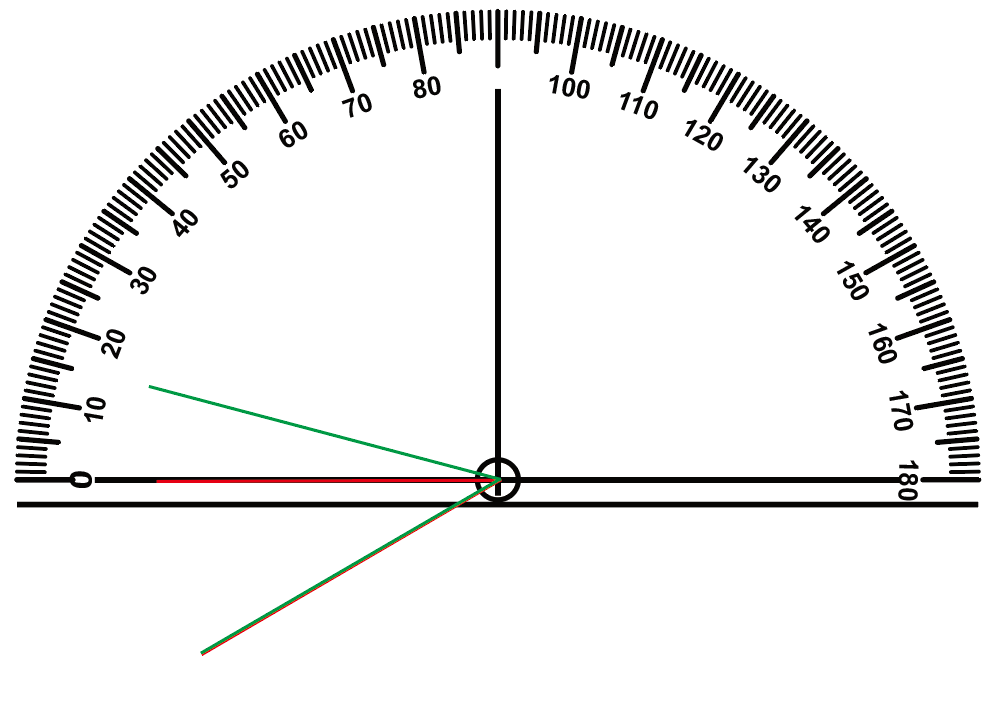
윗부분의 각의 크기는 15도로, 두 각의 크기의 차와 같습니다.
45°-30°=15°
(3) 직각, 예각, 둔각
[정리]
- 직각 : 90°
- 예각 : 0°보다 크고, 90°보다 작은 각
- 둔각 : 90°보다 크고, 180°보다 작은 각
직각을 기준으로 직각보다 작은 각을 예각, 직각보다 큰 각을 둔각이라고 부릅니다.
| 4. 삼각형과 사각형의 각 크기의 합
(1) 삼각형의 세 각의 합
[정리] 삼각형의 세 각의 합은 180°입니다.
삼각형의 세 각의 크기의 합은 세 각의 크기를 각도기로 잰 뒤, 더하는 방법으로 계산할 수 있습니다.
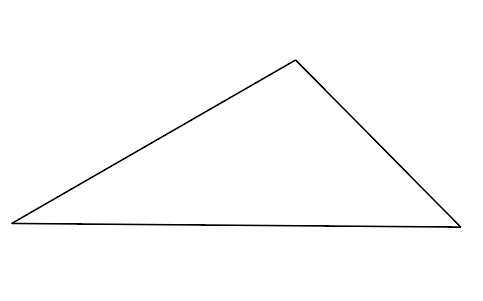
주어진 삼각형의 세 각의 합을 구해봅시다.
30°
45°
105°
삼각형의 세 각 30°, 45°, 105°를 더하면,
30°+45°+105°=180°
(2) 사각형의 네 각의 합
[정리] 사각형의 네 각의 합은 360°입니다.
사각형 역시 삼각형의 세 각의 합을 구하는 방법으로 계산하면 360°를 얻을 수 있습니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지 제작소에 있으며, 비상업적, 상업적 이용이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
#태그 : 각도, 초4, 초등학교 4학년, 각, 각의 크기, 직각, 예각, 둔각, 각의 합, 각의 차, 각도의 덧셈, 각도의 뺄셈, 각도 요점정리, 삼각형 내각의 합, 삼각형 세 각의 합, 사각형 내각의 합, 사각형 네 각의 합, 어림하기
'교과서 정보 + 요점정리 > 초등학교 4학년' 카테고리의 다른 글
| 초등학교 4학년 1학기 과학 교과서 목차(최신판) (0) | 2020.11.19 |
|---|---|
| 초등학교 수학 4학년 1학기 3단원 곱셈과 나눗셈 요점정리 (0) | 2020.07.26 |
| 초등학교 수학 4학년 1학기 1단원 큰 수 요점정리 (0) | 2020.07.17 |
| 초등학교 4학년 2학기 수학 교과서 목차 (최신판) (2) | 2020.01.30 |
| 초등학교 4학년 1학기 수학 교과서 목차 (최신판) (0) | 2020.01.29 |
댓글