
안녕하세요, 학습지제작소입니다.
오늘은 중학교 1학년 문자와 식 학습지를 포스팅하려고 합니다.
지금까지 문자와 식 단원에서 일차방정식, 문자로 나타내기, 식의 값 구하기를 공부했었는데요.
오늘은 일차식을 더하고 빼는 문제를 풀어보려고 합니다.
| 일차식의 의미
일차식을 이해하기 위해서는 항에 대하여 이해할 필요가 있습니다.
항이란, 수 또는 문자의 곱으로 이루어진 식을 의미합니다.

준식은 세 항의 덧셈으로 이루어져 있으며, 항은 각각 2x, -y, 1입니다.
이 중 1은 문자 없이 숫자로만 이루어져 있습니다. 이와 같이 문자가 없이 숫자로만 이루어진 항을 상수항이라고 합니다.
문자가 있는 항 2x, -y은 각각 2와 x, -1과 y가 곱해져 있는데요,
문자와 곱해져 있는 수 (2와 -1)을 계수라고 합니다.
예를 들어 2x의 계수는 2겠죠?
이와 같이 식은 항끼리 더해져 있거나, 항 자체로 존재합니다. 여러 항끼리의 합으로 구성된 식을 다항식, 항 자체로 존재하는 식을 단항식이라고 합니다.
다항식이나 단항식은 문자가 곱해진 횟수를 기준으로 분류할 수 있는데요, 문자가 곱해진 횟수를 차수라고 합니다. 다항식의 경우 항 중 가장 높은 차수를 식의 차수로 가집니다.
다음 여섯 개의 식을 차수에 따라 분류해봅시다.
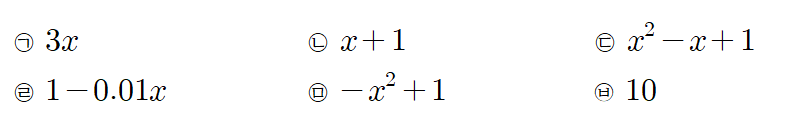
위 여섯 개의 식의 차수를 조사해보면,
㉠은 3과 x가 곱해져 있고, x은 총 1번 곱해져 있으므로 차수가 1입니다.
㉡은 x와 1이 더해져 있고 항 x의 차수가 1이므로 식의 차수는 1입니다.
㉢은 x^2, -x, 1 세 항이 더해져 있고, x^2의 차수는 2, -x의 차수는 1, 1의 차수는 0입니다. 그 중 가장 높은 차수가 2이므로, 이 식의 차수는 2입니다.
㉣은 1과 -0.01x가 더해져 있고, 1의 차수는 0, -0.01x의 차수는 1입니다. 따라서 이 식의 차수는 1입니다.
㉤은 -x^2, 1이 더해져 있고, 각 항의 차수가 2,0이므로, 식의 차수는 2입니다.
㉥은 상수항으로, 차수가 0입니다.
따라서
차수가 0인 식 : ㉥
차수가 1인 식 : ㉠,㉡,㉣
차수가 2인 식 : ㉢,㉤
으로 분류할 수 있습니다. 차수가 1인 식을 일차식, 차수가 2인 식을 이차식이라고 부르는데요,
위 활동에서 분류한 결과를 이야기할 때,
상수항으로만 이루어진 식 : 1개
일차식 : 3개
이차식 : 2개
라고 말할 수 있습니다.
| 일차식의 덧셈, 뺄셈
일차식의 연산은 동류항이라는 항끼리 더할 수 있는데요,
동류항이란 항에서 계수를 제외한 부분(문자로 이루어진 부분)이 서로 같은 항을 말합니다.
만약 2x+2y-1+y를 계산한다면, 동류항은 2y와 y밖에 없습니다.
2x와 2y, 2y와 -1끼리는 더할 수 없죠.
동류항끼리 더하고 뺄 때는 계수끼리 더하거나 빼면 됩니다.
2y+y를 계산한다면 2y의 계수인 2와 y의 계수인 1을 더한 후, 계수 3을 y와 붙여 나타내면 됩니다.
따라서 2x+3y-1로 표현할 수 있습니다.
이와 같이 일차식의 덧셈과 뺄셈은 다음과 같은 방법으로 풀 수 있습니다.
i) 괄호를 푼다.
ii) 동류항을 찾는다.
iii) 동류항의 계수끼리 더하거나 빼어 하나로 나타낸다.
예) -3(x-6)+(x+1)을 풀기위해 괄호를 풀면,
-3x+18+x+1입니다. 준식의 동류항은 -3x와 x, 18과 1이므로
동류항끼리 더하면,
-2x와 19가 됩니다.
따라서 -2x+19입니다.
답 : -2x+19


이번 학습지는 일차식의 의미를 이해하고, 일차식끼리 정리할 수 있는 문제로 준비했습니다. 특히 괄호를 분배하는 유형 위주로 준비하여 분배법칙과 동류항끼리 더하는 활동 모두 할 수 있도록 구성하였습니다.
학습지 첨부파일은 아래에 있습니다.
[20220402 추가] 답안지 일부에 오류가 있어 수정하였습니다.
학습지를 풀어보면서 일차식의 계산에 능숙해지시길 바랍니다. 일차식의 계산은 앞으로 여러 식을 정리하는 데 기본기이기 때문에 같은 유형의 문제를 꾸준히 풀어 익숙해질 필요가 있습니다.
일차식의 계산 포스팅은 여기서 마치겠습니다. 감사합니다.
#태그 : 일차식의 연산, 일차식의 덧셈, 일차식의 뺄셈, 일차식의 곱셈, 일차식의 나눗셈, 일차식 연산 문제, 중1 수학 문제, 중1 문자와 식 문제, 중1 무료 학습지, 일차식 무료 문제, 분배법칙, 일차식, 이차식, 상수항, 차수, 계수, 단항식, 다항식
'수학 학습지 > 중학교 1학년 1학기' 카테고리의 다른 글
| 소인수분해의 의미와 방법 (개념+수학문제) (0) | 2020.04.20 |
|---|---|
| 치환된 식을 일차식으로 정리하기 (개념 + 연산문제) (0) | 2020.03.23 |
| 둘 이상의 문자가 들어간 식의 값 구하기 (개념+수학문제) (0) | 2020.03.09 |
| 문자와 식 : 식의 값 구하기 (개념+수학문제) (0) | 2020.03.08 |
| 문자로 곱셈식과 나눗셈식 간단히 나타내기 (개념+수학문제) (3) | 2020.03.04 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 3. 16.
2020. 3. 16. 댓글
댓글
