
* 수정사항 안내
[2020-12-20 수정] 문제 일부의 답이 잘못 표기되어 있어 고쳤습니다. 학습지에서 수식으로 적혀있지 않은 부분을 고쳤습니다.
안녕하세요, 학습지제작소입니다.
오늘은 고등수학(상)의 다항식 단원의 나머지정리를 공부할 차례입니다.
저번 학습지까지는 인수분해를 공부하면서, 다항식을 여러 인수들의 곱으로 표현해보았는데요,
오늘은 다항식을 차수가 낮은 다항식으로 나누었을 때 나머지를 어떻게 구할 수 있는지 이야기해보겠습니다.
| 항등식의 성질은 무엇일까?
나머지정리를 본격적으로 배우기 전에, 항등식에 대한 논의가 필요합니다.
항등식이란 어떤 변수 x에 대하여 다항식 P(x), Q(x)가 x의 값에 관계없이 항상 같은 식을 의미합니다.

위 두 다항식 P(x), Q(x)에 대하여 두 식은 x에 어떤 값을 넣더라도 값이 항상 같습니다.
따라서 P(x) = Q(x)는 항등식입니다.
그렇다면, 항등식의 성질은 무엇일까요?
항등식의 성질은 좌변과 우변의 계수들이 모두 서로 같다는 점입니다.
위 P(x)와 Q(x)를 비교해보아도 x의 계수가 각각 3, 상수항이 각각 -1입니다.
이러한 성질을 이용해, 항등식인 식에 관해 문자의 값을 구할 수도 있습니다.
<예제 1>
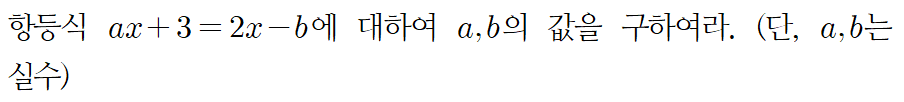
위 예제에 대하여 등식 ax+3=2x-b는 항등식입니다.
이때 x의 계수는 a와 2로 서로 같고, 상수항은 3과 -b로 서로 같습니다.
따라서

을 얻을 수 있습니다.
| 나머지정리란 무엇일까?
나머지정리란, 다항식 P(x)를 x-a, 즉 일차식으로 나누었을 때 나머지 R에 대하여 다음 식이 성립한다는 정리입니다.

어떻게 이러한 공식을 얻을 수 있을까요? 한 번 P(x)를 x-a로 나누어보겠습니다. 이때 몫을 Q(x)라고 약속한다면,
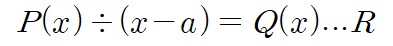
라고 표현할 수 있습니다. 이를 검산식으로 나타내면,

이 됩니다. 고등수학에서는 일반적으로 나눗셈을 나눈 식과 몫의 곱과 나머지의 합으로 나타냅니다.
이 상태에서 x=a를 대입해봅시다.

위 식에서 a-a는 0이므로, R을 뺀 나머지 부분은 0이 됩니다.

따라서 나머지 R은 x-a에 대하여 x=a일 때 다항식 P(x)의 값입니다.
즉 나머지 정리는,
나누는 수가 0이 되게 만드는 x의 값을 대입한 식의 값입니다.
이해를 위해 예제 두 문제를 풀어봅시다.
<예제 2>

<예제 2>를 풀기 위해 P(x)를 x+1로 나누어보면,
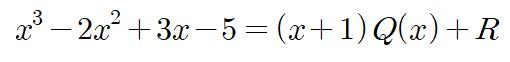
로 표현할 수 있습니다. 이 상태에서 x에 -1을 대입하면,

이 되어 나머지가 -11임을 알 수 있습니다.
<예제 3>

<예제 2>를 풀기 위해 나머지정리 꼴로 나타내면,

입니다. 2x-1을 0으로 만드는 x의 값은 1/2이기 때문에 x=1/2를 양변에 대입합니다.

따라서 나머지는 -1/4입니다.
이번 연습문제는 모두 삼차식을 일차식으로 나누었을 때 나머지를 구하는 문제들입니다. 나머지정리를 이용해 나머지를 구해보시길 바랍니다.

학습지 첨부파일은 아래에 있습니다.
그럼 나머지정리 첫 번째 포스팅을 마치겠습니다.
다음 포스팅은 이차식으로 나누었을 때 나머지 구하기 문제로 찾아뵙겠습니다.
감사합니다!
#태그 : 고등학교 1학년 수학, 고1 수학, 고등수학(상), 고등수학, 나머지정리, 다항식, 나머지정리 하는 방법, 나머지정리 공식, 나머지정리 연습문제, 고1 수학 연산문제, 고1 수학, 다운, 다운로드, pdf
'수학 학습지 > 공통수학1' 카테고리의 다른 글
| 인수정리 (고등수학(상) 개념+수학문제) (0) | 2020.03.29 |
|---|---|
| 나머지정리 (2) : 이차식으로 나눈 나머지 구하기 (개념+연산문제) (0) | 2020.03.14 |
| 곱셈공식을 활용한 인수분해 (고등수학(상) 개념+수학문제) (0) | 2020.02.24 |
| 조립제법을 활용한 인수분해 (개념+수학문제) (0) | 2020.02.11 |
| 고등수학(상) 다항식의 전개 수학문제 다운로드 (0) | 2020.01.29 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 3. 6.
2020. 3. 6. 댓글
댓글
