안녕하세요, 학습지제작소입니다.
이 카테고리(이하 보충자료)에 올리는 보충자료라 함은,
현재 연재 중이지 않고 이전에 사용했던 학습지자료로 해당 진도 관련 문제를 풀고 싶거나, 보충문제를 찾으시는 선생님들께 공유하고자 올리는 자료입니다.
따라서 보충자료는 연재를 시작하지 않는 이상 새로운 문제가 업로드되지 않으니 양해의 말씀드립니다.
오늘은 중학교 2학년 수학문제를 포스팅해보려고 하는데요,
현재 연재하고 있는 이 카테고리는 2020SP M2로,
중학교 2학년 학생을 대상으로 2020년에 연재하는 연산보충자료입니다.
앞서, 연립방정식 2부를 업로드한 바 있는데요,
[중2/수학문제] 1. 연립방정식 (1)
안녕하세요, 학습지제작소입니다. 이 카테고리(이하 보충자료)에 올리는 보충자료라 함은, 현재 연재 중이지 않고 이전에 사용했던 학습지자료로 해당 진도 관련 문제를 풀고 싶거나, 보충문제를 찾으시는 선생님..
calcproject.tistory.com
[중2/수학문제/보충자료] 2. 연립방정식 (2)
안녕하세요, 학습지제작소입니다. 이 카테고리(이하 보충자료)에 올리는 보충자료라 함은, 현재 연재 중이지 않고 이전에 사용했던 학습지자료로 해당 진도 관련 문제를 풀고 싶거나, 보충문제를 찾으시는 선생님..
calcproject.tistory.com
연립방정식 문제를 보고싶거나 풀어보고 싶으신분들은 위 링크를 활용하시길 바랍니다.
3번 학습지부터는 중학교 2학년 진도에 맞추어 연재할 계획인데요,
유리수와 순환소수, 식의 계산, 일차부등식, 연립방정식(나머지), 일차함수 순서로 연습문제를 다뤄보고 싶습니다.
유리수와 순환소수는 첫 번째 단원으로, 연습문제가 있으면 분수를 소수로, 소수를 분수로 나타내는 연습이 될 수 있으리라고 생각합니다.
* 오늘의 주제는 무엇인가요?
오늘의 주제는 유한소수와 무한소수 구별하기입니다.
즉, 분수를 주고 이것이 유한소수인가 무한소수인가 구분하는 내용을 담고 있습니다.
이를 이해하기 위해서는 유한소수와 무한소수를 공부할 필요가 있는데요,
우선 유리수를 알아보겠습니다.
1. 유리수의 정의
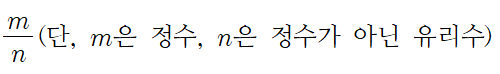
유리수는 두 정수 m과 n에 대해 위 정의를 만족하는 모든 수입니다. 쉽게 말해, 분모가 0이 아닌 분수로 나타낼 수 있는 모든 수를 의미하죠.
예)
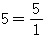
은 분모가 0이 아닌 분수로 나타낼 수 있으므로, 유리수입니다.

은 분모가 3이고, 분자가 10이므로, 유리수입니다.

은 분모가 1이고, 분자가 -3이므로, 유리수입니다.
(+ 이를 통해 모든 정수는 분모가 1인 유리수 꼴로 표현이 가능하며, 모든 정수는 유리수임을 알 수 있죠.)
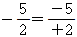
은 분모가 +2이고, 분자가 -5이므로, 유리수입니다.
2. 유한소수와 무한소수
(1) 분수와 소수의 관계
이렇게 모든 유리수는 분수로 나타낼 수 있게 되는데, 분수와 소수의 관계를 논의해 볼 필요가 있습니다.
초등학교에서 처음으로 소수를 공부할 때, 우리나라 교육과정에서는 다음을 기준으로 삼고 있습니다(이하 교육과정).
분모가 10인 진분수를 통하여 소수 한 자리 수를 이해하고 읽고 쓸 수 있다.
교육과정에 근거했을 때, 소수 한 자리 수는 분모가 10인 진분수에서 나타냄을 알 수 있죠.

이 그림은 막대 하나를 10등분한 뒤, 3만큼 색칠한 것입니다.
우리는 이것을 분수로, 나타낼 수 있고, 다음과 같이 고칠 수 있죠.

소수 첫째 자리를 배우고 나면, 소수 둘째 자리와 셋째 자리를 배우게 됩니다. 이 역시 분모를 100, 1000으로 나타내어 표현을 하게 됩니다.

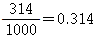
(2) 유한소수
우리는 이 과정에서 분모를 살펴볼 필요가 있습니다. 분모가 10, 100, 1000일 때 분자의 숫자와 소수 자릿수에 적혀 있는 숫자는 일치합니다. 즉, 분모가 10의 제곱 꼴이라면 소수점 아래에 0이 아닌 숫자가 유한한 분수로 나타낼 수 있죠. 이를 유한소수라고 합니다.
더 나아가보면, 10의 제곱 꼴은 자연수 n에 대하여

꼴로 표현할 수 있고, 이를 소인수분해하면
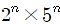
꼴을 얻을 수 있습니다. 이는 기약분수의 소인수가 2 또는 5밖에 없다면 유한소수로 나타낼 수 있다는 뜻입니다.
예)

은 분모의 소인수가 2와 5이므로 유한소수입니다.

은 분모의 소인수가 2와 5이므로, 적절한 수(5)를 곱하면 10의 제곱꼴로 나타낼 수 있습니다. 따라서 유한소수입니다.
(3) 무한소수
무한소수는 소수점 아래의 자리중 0이 아닌 숫자가 끊임없이 생기는 소수를 의미합니다.
정의에서 0이 아닌 숫자가 거론되는 까닭은

과 같이 0이 반복되는 것은 유한소수로 나타낼 수 있기 때문입니다.
무한소수는 기약분수의 분모가 2또는 5가 아닌, 그 외의 소인수가 있는 경우입니다.
유한소수를 나타낼 때는 소인수로 2만 있거나, 5만 있는 경우도 가능했지만, 무한소수는 기약분수의 분모 중 그 외 소인수가 하나라도 있으면 됩니다. 이를 표로 나타내면 다음과 같습니다.

예)

은 분모의 소인수 중 3이 있으므로 무한소수입니다. (0.333333...)

은 분모의 소인수가 2,3인데, 소인수 중 3이 있으므로 무한소수입니다. (0.166666...)
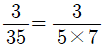
은 분모의 소인수가 5,7인데, 소인수 중 7이 있으므로, 무한소수입니다. (0.08571428571428...)
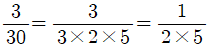
은 분모의 소인수가 2,3,5이지만, 기약분수로 나타내면 3이 사라지므로 유한소수입니다.
이와 같이 기약분수인지 아닌지 판단한 후, 소인수를 살펴보면 유한소수인지 무한소수인지 알 수 있습니다.
학습지제작소에서는 여러 가지 분수를 주고 유한소수인지 무한소수인지 판단해볼 수 있게 학습지를 준비했습니다.
<미리 보기>




중학교 수준에서 나올 수 있는 분수를 제시하고, 빈칸에 알맞은 답을 쓰는 학습지입니다.
학습지 파일은 다음과 같습니다.
오늘도 여러분들의 수학 공부에 힘이 되었으면 좋겠습니다!
감사합니다.
#태그 : 유리수와 순환소수 문제 / 유리수 문제 / 순환소수 문제 / 중학교 2학년 수학 문제 / 유한소수 무한소수 문제 / 다운 / 다운로드 / 문제 다운로드 / 무료 / 유리수와 순환소수 pdf / 중학교 2학년 수학 pdf / 유한소수 문제 / 무한소수 문제 / 중2 수학 문제
※ 저작물 관련 유의사항
- 본 저작물(문제 및 그림)은 학습지 제작소에 있으며, 비상업적, 상업적 이용이 가능합니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
Copyright. 2020. 학습지제작소. All Rights Reserved.
'수학 학습지 > 중학교 2학년 1학기' 카테고리의 다른 글
| [중2-1] 6. 유리수와 순환소수 > 순환소수를 분수로 나타내는 법 (개념+수학문제) (0) | 2020.03.02 |
|---|---|
| [중2-1] 5. 유리수와 순환소수 > 순환소수로 나타내기 (2) (개념+수학문제) (0) | 2020.02.28 |
| [중2-1] 4. 유리수와 순환소수 > 순환소수로 나타내기 (개념+수학문제) (0) | 2020.02.21 |
| [중2-1] 2. 연립방정식 (2) (수학문제) (0) | 2020.02.13 |
| [중2-1] 1. 연립방정식의 풀이 : 가감법, 대입법 (개념+수학문제) (1) | 2020.02.06 |

 학습지제작소 관리자
학습지제작소 관리자 2020. 2. 17.
2020. 2. 17. 댓글
댓글
