[중3-1] 곱셈공식을 이용하여 입체도형의 겉넓이와 부피 구하기

* 같이 보면 좋은 글

• 곱셈공식

• 곱셈공식을 이용한 수의 계산, 분모의 유리화

---

* 곱셈공식을 이용하여 입체도형의 겉넓이와 부피 구하기

문제 세 모서리의 길이가 x+1, 3, x-1인 직육면체가 있다. 이 직육면체의 겉넓이는? (단, x>1)

풀이

모서리의 길이가 $a,b,c$ 직육면체의 겉넓이가 $2(ab+bc+ca)$임을 이용하면,

$2 \left\{ 3(x - 1) + 3(x + 1) + (x - 1)(x + 1) \right\}$

$= 2 \left( 3x - 3 + 3x + 3 + x^2 - 1 \right) \\
= 2(x^2 + 6x - 1) \\
= 2x^2 + 12x - 2$

 

300x250

 

이처럼 입체도형의 겉넓이/부피를 구하는 방법을 알고 있으면 x를 미지수로 하는 식이라도 구할 수 있습니다.

* 가로가 a, 세로가 b, 높이가 c인 직육면체의 겉넓이: $2(ab+bc+ca)$

* 가로가 a, 세로가 b, 높이가 c인 직육면체의 부피: $abc$

* 밑면이 S, 높이가 h인 각기둥의 부피: $Sh$

* 밑면이 S, 높이가 h인 각뿔의 부피: $\cfrac{Sh}{3}$
* 반지름의 길이가 r인 구의 겉넓이: $4 \pi r^2$
* 사각뿔대의 부피: (자르기 전 사각뿔의 부피) - (자른 사각뿔의 부피)

 

문제 가로의 길이가 x-1, 세로의 길이가 x+1, 높이가 a인 직육면체가 있다. 이 직육면체의 모든 모서리의 길이의 합이 24일 때, 이 직육면체의 겉넓이는? (단, 1<x<3)

풀이

직육면체의 모든 모서리의 길이의 합을 구하면

$4(x - 1 + x + 1 + a) = 24, a=6-2x$

$a$에 $6-2x$를 대입해 계산하면,

$2 \left\{ (x - 1)(x + 1) + (x + 1)(6 - 2x) + (x - 1)(6 - 2x) \right\} \\
= x^2 - 1 + (-2x^2 + 4x + 6) + (-2x^2 + 8x - 6) \\
= x^2 - 2x^2 - 2x^2 + (4x + 8x) + (-1 + 6 - 6) \\
= -3x^2 + 12x - 1$

여기에 2를 곱하면 $-6x^2 +24x -2$입니다.

 

문제 다음 사각뿔대의 부피를 구하시오. (단, 아랫면은 정사각형이다.)

사각뿔대의 부피 구하기

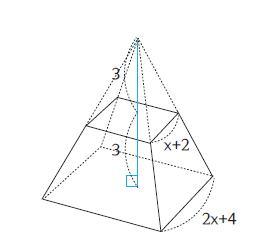
풀이

사각뿔대는 자르기 전 사각뿔의 부피에서 자른 사각뿔의 부피를 빼 부피를 구할 수 있습니다.
● 자르기 전 사각뿔의 부피
$= (2x + 4)^2 \times 6 \times \frac{1}{3} = 2(2x + 4)^2 \\
= 2(4x^2 + 16x + 16) \\
= 8x^2 + 32x + 32$

● 자른 사각뿔의 부피
$= (x + 2)^2 \times 3 \times \frac{1}{3} = (x + 2)^2 \\
= x^2 + 4x + 4$

● 남은 사각뿔대의 부피

$(8x^2 + 32x + 32) - (x^2 + 4x + 4) \\
= 7x^2 + 28x + 28$

---

* 학습지 미리보기

입체도형의 겉넓이와 부피

---

---

 

 

중3 곱셈공식 연습문제

 

---

* 첨부파일

2025TS M3-01(곱셈공식을 이용한 입체도형의 겉넓이와 부피 구하기)_문제지+정답지.pdf

0.26MB

 

곱셈공식을 이용한 입체도형의 겉넓이와 부피 유형을 준비했습니다.

모두 10문제이며 식을 세워보고 정리해보며 문제를 풀어봅시다.

300x250

 

 

✔ 이 글이 도움이 되셨나요?

- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.

 

✔ 저작물 관련 유의사항

- 본 저작물(문제 및 도형 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.

- 다른 사진을 참조한 경우, 파일 마지막 페이지에 출처를 밝히고 있습니다.

- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.

- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.

Copyright. 2025. 학습지제작소. All Rights Reserved.

 

#태그 : 중3, 중학교 3학년, 곱셈 공식, 입체도형의 겉넓이와 부피 유형