학습지제작소 관리자
2025. 7. 15.* 같이 보면 좋은 글
* 삼각형의 넓이
삼각형에서 한 변을 밑변으로 놓을 때,
맞은 편 꼭짓점과 수직을 이루는 선분의 길이를 높이라고 합니다.
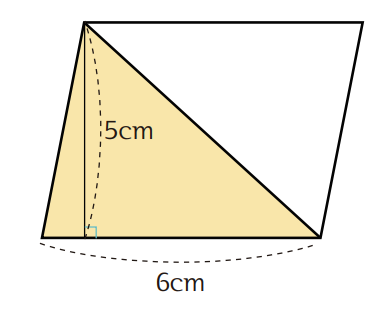
위와 같은 평행사변형이 있을 때 평행사변형의 밑변의 길이와 높이는 각각 얼마입니까?
** 평행사변형의 밑변의 길이는 6cm입니다.
** 평행사변형의 높이는 5cm입니다.
이 평행사변형에서 대각선을 그어 삼각형을 만들었을 때, 삼각형의 밑변의 길이와 높이는 각각 얼마입니까?
** 삼각형의 밑변의 길이는 6cm입니다.
** 삼각형의 높이는 5cm입니다.
이처럼 색칠한 부분(삼각형)은 기존의 평행사변형과 밑변의 길이, 높이가 각각 같습니다.
그렇다면 삼각형의 넓이를 구해볼까요?
(평행사변형의 넓이)=(밑변의 길이)×(높이)
였습니다. 따라서 평행사변형의 넓이는
$6cm × 5cm = 30cm^2$
삼각형의 넓이는 평행사변형 넓이의 반이었으므로
$6cm × 5cm ÷ 2 = 15cm^2$
따라서 삼각형의 넓이는
(삼각형의 넓이) = (평행사변형의 넓이)÷2 = (밑변의 길이)×(높이)÷2
예) 밑변의 길이가 10cm, 높이가 5cm인 삼각형의 넓이는
$10×5÷2=25cm^2$
예) 밑변의 길이가 12cm, 높이가 8cm인 삼각형의 넓이는
$12×8÷2=48cm^2$
삼각형의 넓이와 관련한 여러 가지 문제를 해결해봅시다.
문제 삼각형의 높이를 표시해보세요.
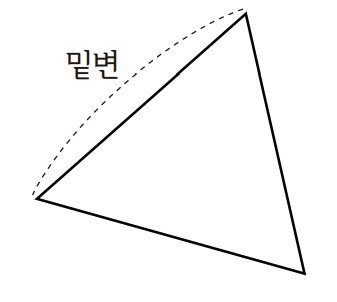
풀이
삼각형의 높이는 밑변과 마주하는 꼭짓점을 지나면서 밑변과 수직인 선분의 길이입니다.
밑변과 마주한 꼭짓점에서 수직으로 선분을 내리면
위와 같이 나타낼 수 있습니다.
문제 다음 삼각형의 넓이가 $24cm^2$일 때, 빈칸에 들어갈 수를 써넣으세요.
풀이
밑변의 길이가 □cm, 높이가 8cm이므로 삼각형의 넓이를 구하기 위한 식을 세우면,
$□ × 8 ÷ 2 = 24$입니다.
□의 값을 구하면 6이므로 빈칸에 들어갈 수는 6입니다.
문제 빈칸에 들어갈 수를 써넣으세요.
풀이
밑변의 길이를 20cm로 놓으면 높이는 15cm이므로
삼각형의 넓이는 20×15÷2=150cm²입니다.
150=25×□÷2이기도 하므로
□=12입니다.
* 학습지 미리보기
* 첨부파일
초등학교 5학년 1학기 수학 중
삼각형의 넓이 연습문제를 올립니다. 모두 15문제이며,
삼각형의 넓이를 구하는 과정을 살펴보며 익혀보길 바랍니다.
✔ 이 글이 도움이 되셨나요?
- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.
✔ 저작물 관련 유의사항
- 본 저작물(문제 및 도형 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.
- 다른 사진을 참조한 경우, 파일 마지막 페이지에 출처를 밝히고 있습니다.
- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.
- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.
Copyright. 2025. 학습지제작소. All Rights Reserved.
#태그 : 초5, 초등학교 5학년, 삼각형의 넓이 구하는 법, 삼각형의 넓이 공식 설명, 삼각형 넓이 문제
'수학 학습지 > 초등학교 5학년 1학기' 카테고리의 다른 글
| [초5-1] 사다리꼴의 넓이 구하는 법, 공식, 사다리꼴 넓이 연습문제 수학학습지 (0) | 2025.07.19 |
|---|---|
| [초5-1] 평행사변형의 넓이 구하는 법, 공식 (초등수학 개념정리, 연습문제) (3) | 2025.07.04 |
| [초5-1] 1제곱센티미터(1cm^2)를 알아볼까요 | 넓이 개념정리 수학학습지 (1) | 2025.07.02 |
| [초5-1] 평행사변형의 둘레, 마름모의 둘레 - 다각형의 둘레와 넓이 단원 개념정리 연습문제 학습지 (2) | 2025.06.28 |
| [초5-1] 분수의 덧셈과 뺄셈 > 어떤 수 문제, 잘못 계산한 유형, 바르게 계산하기 수학학습지 연습문제 (2) | 2025.06.27 |
댓글
