[초6 수학] 직육면체의 부피, 정육면체 부피 구하는 법 요점정리+수학학습지 연습문제

* 같이 보면 좋은 글

 

• 띠그래프

• 원그래프

---

* 1cm^3(1세제곱센티미터)를 알아볼까요

부피란, 입체도형이 차지하는 공간의 양을 말합니다.

넓이를 측정할 때 길이가 1cm인 정사각형이 몇 개인지 바탕으로 계산했듯이,

부피를 측정할 때에도 기준이 되는 도형이 몇 개인지 세어볼 수 있습니다.

 

1세제곱센티미터

 

부피를 측정할 때에는 한 모서리의 길이가 1cm인 정육면체가 몇 개인지를

바탕으로 구할 수 있습니다.

이때 한 모서리의 길이가 1cm인 정육면체의 부피를 $1cm^3$라 쓰고, 1제곱센티미터라고 읽습니다.

 

문제 그림과 같이 부피가 $1cm^3$인 쌓기나무를 이용하여 직육면체의 부피를 구하세요.

직육면체의 부피 구하기

풀이

직육면체에서 1층은 쌓기나무가 몇 개입니까?

쌓기나무의 가로가 3칸, 세로가 2칸이므로 $3×2=6$개입니다.

직육면체가 2층까지 있으므로

$6×2=12$개입니다.

따라서 $12cm^3$입니다.

 

300x250

 

문제 다음 그림과 같이 가로의 길이가 4cm, 세로의 길이가 3cm, 높이가 2cm인 직육면체의 부피를 구해봅시다.

직육면체의 부피 구하기

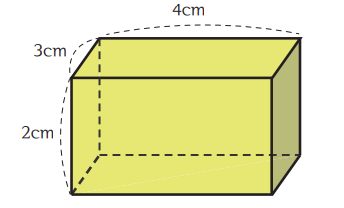
풀이

한 모서리의 길이가 1cm인 쌓기나무로 직육면체를 채워봅시다.

쌓기나무로 직육면체를 채우면 1층에는

가로 4칸, 세로 3칸으로 12개의 쌓기나무를 채울 수 있습니다.

 

직육면체의 높이가 2cm이므로 12개의 쌓기나무에 2를 곱하면 $24cm^3$가 됩니다.

 

부피를 구하는 과정을 간단하게 하면 가로가 1cm가 4개, 세로가 1cm가 3개, 높이가 1cm가 2개이므로

$4×3×2=12×2=24cm^3$로 계산할 수도 있습니다.

 

 

문제 다음 그림과 같이 한 모서리의 길이가 4cm인 정육면체가 있습니다. 부피를 구해봅시다.

정육면체의 부피 구하기

 

풀이

같은 방법으로 한 모서리의 길이가 1cm인 쌓기나무로 직육면체를 채워봅시다.

쌓기나무로 직육면체를 채우면 1층에는

가로 4칸, 세로 4칸으로 16개의 쌓기나무를 채울 수 있습니다.

 

직육면체의 높이가 4cm이므로 16개의 쌓기나무에 4를 곱하면 $64cm^3$가 됩니다.

 

이를 정리하면 정육면체는 가로, 세로, 높이가 서로 같으므로

한 모서리의 길이를 세 번 곱하여 구할 수 있습니다.

따라서 $4×4×4=16×4=64cm^3$로 계산할 수 있습니다.

 

정리 직육면체와 정육면체의 부피 구하기

(1) 직육면체의 부피: (가로)×(세로)×(높이)

(2) 정육면체의 부피: (한 모서리의 길이)×(한 모서리의 길이)×(한 모서리의 길이)

예) 가로가 10cm, 세로가 5cm, 높이가 4cm인 직육면체의 부피는

  ➔ $10×5×4=200cm^3$

예) 한 모서리의 길이가 5cm인 정육면체의 부피는

  ➔ $5×5×5=125cm^3$

---

* 학습지 미리보기

직육면체의 부피 구하기 학습지

---

반응형

---

 

 

 

 

초6 직육면체 정육면체 부피 문제 모음

---

* 첨부파일

2025TS E6-09(직육면체의 부피)_문제지.pdf

0.49MB

 

2025TS E6-09(직육면체의 부피)_정답지.pdf

0.56MB

 

초등학교 6학년 1학기 마지막 단원 '직육면체의 부피와 겉넓이' 단원의 첫 내용인

직육면체/정육면체의 부피 구하기 학습지를 올립니다.

 

가정과 학교에서 많은 사용 부탁드립니다.

감사합니다.

 

300x250

 

✔ 이 글이 도움이 되셨나요?

- 댓글이나 자유게시판에 글을 남겨주세요. 글쓴이에게 큰 힘이 됩니다.

 

✔ 저작물 관련 유의사항

- 본 저작물(문제 및 도형 그림)은 학습지제작소에 있으며, 비상업적, 상업적 이용(수업에서 부교재로 사용하는 경우만)이 가능합니다.

- 다른 사진을 참조한 경우, 파일 마지막 페이지에 출처를 밝히고 있습니다.

- 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.

- 학습지제작소의 저작물을 관리자의 동의없이 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.

Copyright. 2025. 학습지제작소. All Rights Reserved.

 

#태그 : 초6, 초등학교 6학년, 직육면체 부피 구하는 법, 정육면체 부피 공식, 직육면체 부피 문제, 초6 부피 문제